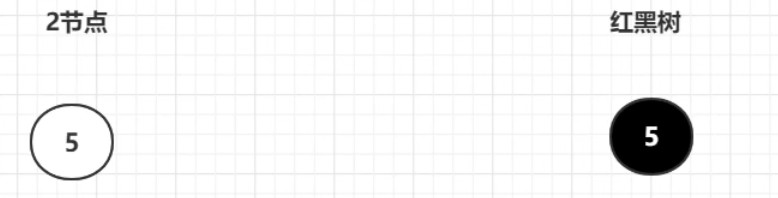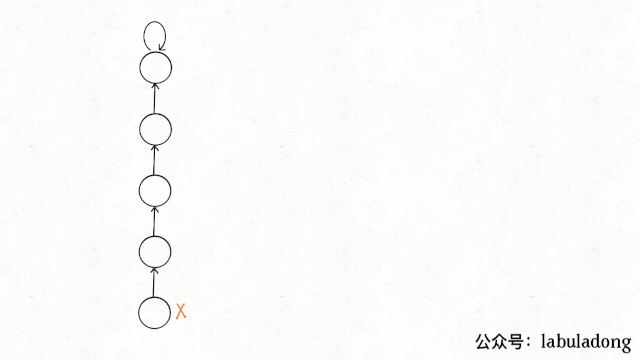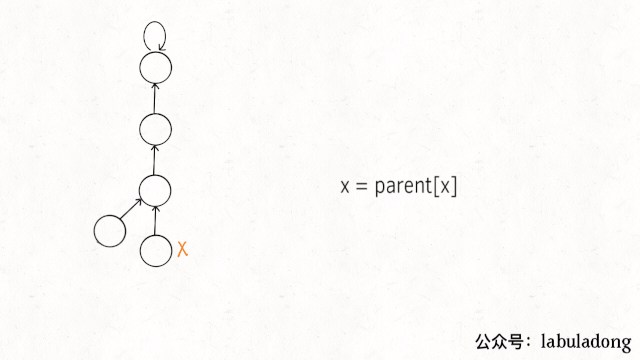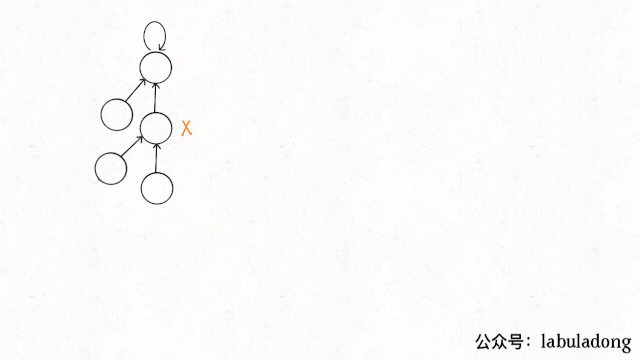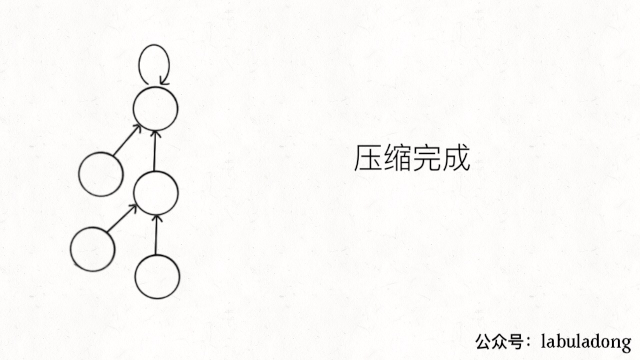树结构
参考博客:
1. 基本概念
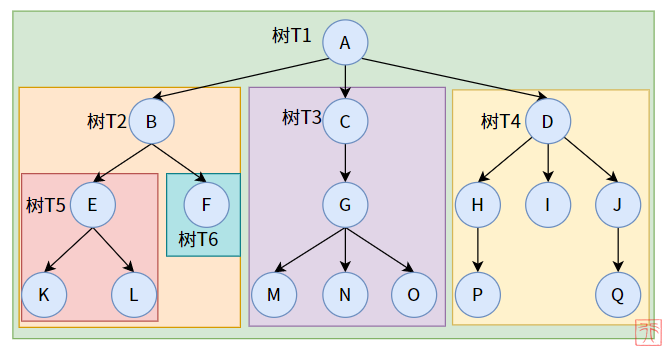
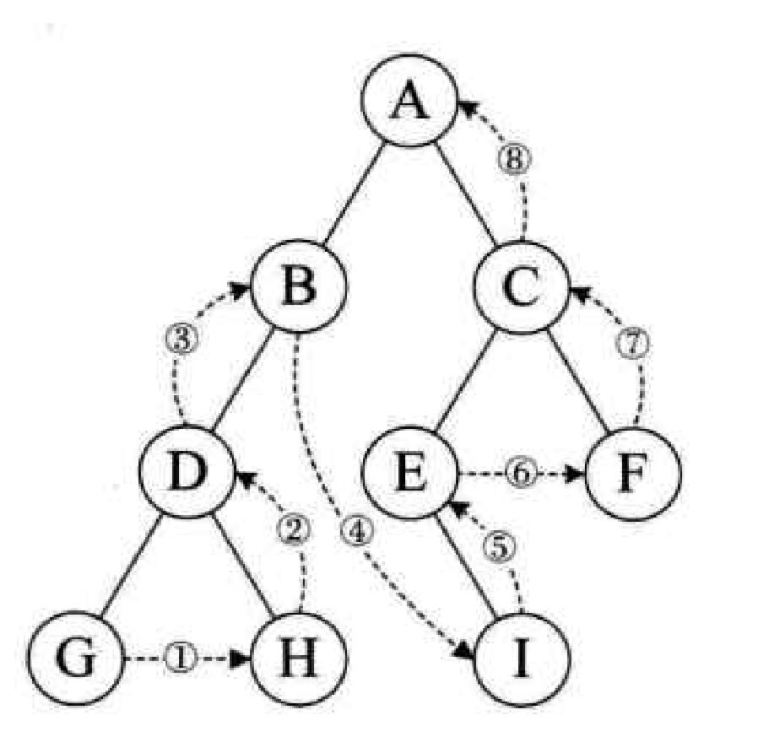
- 子树: 树集合中的一个子集,如图所示。
- 节点(node): 一个结点包括一个数据元素和若干指向其子树分支。
- 根节点(node): 一颗树只有一个树根
- 度(Degree): 一个结点拥有的子树数;例如结点
A的度为3,结点H的度为1 - 叶子(Leaf): 度为
0的结点被称为叶子结点 - 分支结点: 度不为
0的结点 - 内部结点: 在树内部的结点,即不是根结点和叶子结点的结点。
- 层次(Level): 从根结点开始,同辈分的节点为一层; 起始编号为
1;例如节点E在第3层 - 深度(Depth)/ 高度: 指树的最大层次
- 有序树: 结点的各子树从左到右是有次序的、不能颠倒,则为有序树
2. 树的递归特性
[!tip] 树的层级关系可以用来描述一个「族谱」:
- 父结点: 层级靠前的结点
- 子结点: 层级为与父结点相连的下一层的节点。
- 兄弟结点: 同一层级的结点
[!note] 递归特性:
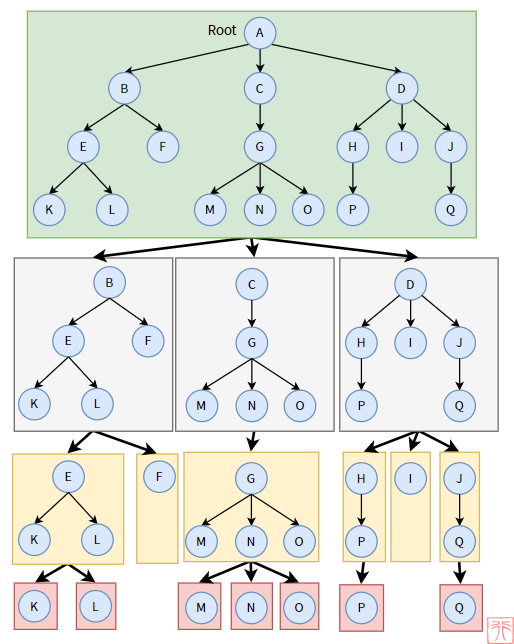
- 在树中,子树仍是一颗树,子树的子树仍是一棵树。(保证存储数据类型是一样的;数据的结构是一样的)
- 父结点下存在子结点(
null,也可以视为一个子结点),对于子结点又可成以成为子树的父结点。(保证存储数据间的关系是类似的,可以利用同一个代码逻辑进行问题处理)
// 传入一颗以root为根结点的树
void recursion(Node* root){
业务逻辑处理
// 子结点又是子树的根结点
recursion(root->child);
}
3. 二叉树
3.1. 基本概念
[!note|style:flat] 定义:限制了孩子数量,即每个结点最多只能有两个孩子(左孩子和右孩子)
- 第
k层的结点数: 。 - 深度为
h的二叉树的总结点数:
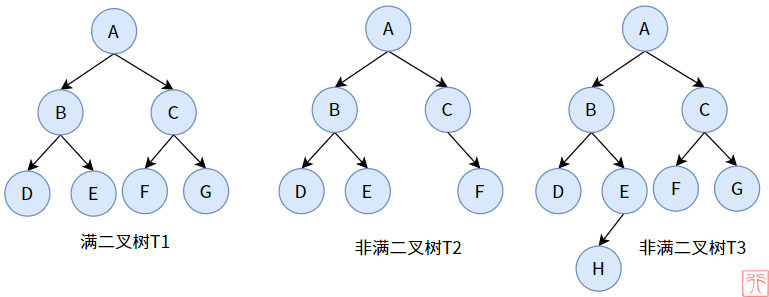
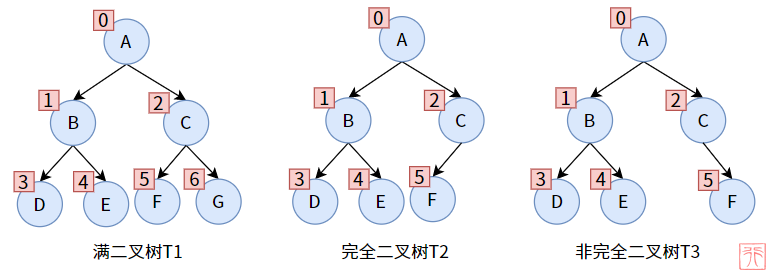
3.2. 满二叉树 full binary Tree
[!note|style:flat] 定义:一个二叉树的深度为
h,且结点总数是 ;一棵二叉树的结点要么是叶子结点,要么该结点有两个子结点
3.3. 完全二叉树 complete binary tree
[!note|style:flat] 定义:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。
3.4. 满二叉树与完全二叉树
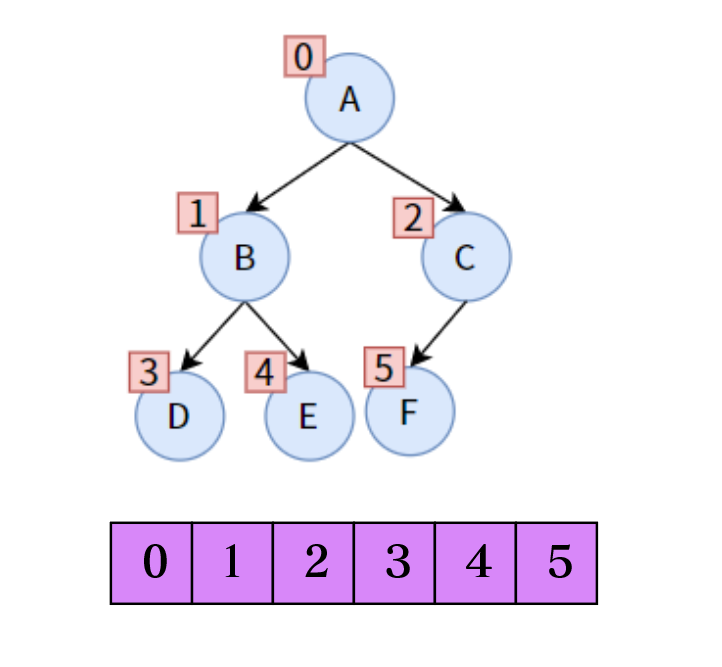
[!note] 对于满二叉树与完全二叉树,一般可以采用「数组」的形式进行存储。
- 父节点的编号为
k,子左节点编号为2k,子右节点的编号为2k+1 - 子节点的编号为
x,父节点的编号为 - 从上往下最后一个父节点的编号为 (
n为总节点数)
4. 二叉树遍历
4.1. 遍历框架
- 前序遍历
- 中序遍历
- 后序遍历
void Traversal(Node* root){
// 退出条件
if(root == nullptr) return;
// 前序遍历
Traversal(root->left);
// 中序遍历
Traversal(root->right);
// 后序遍历
}
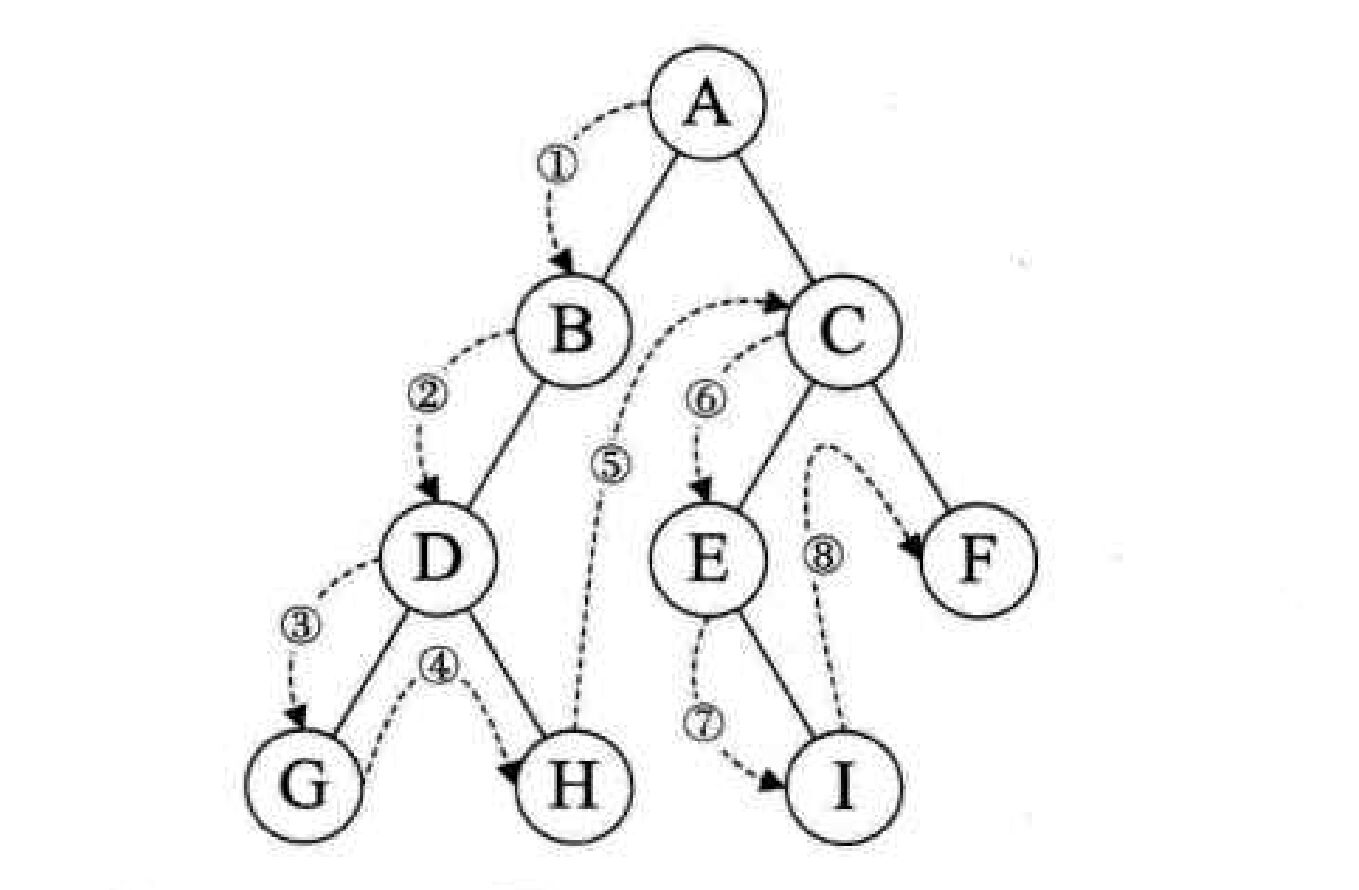
4.2. 前序遍历
[!tip] 以当前节点作为根节点的子树
- 当前结点先输出,再进入「左子结点」
- 若「左子结点」为
null,则回退「父结点」- 然后再进入「右子结点」
- 若「右子结点」为
null,则回退「父结点」- 「右子结点」查询完,返回「父结点」
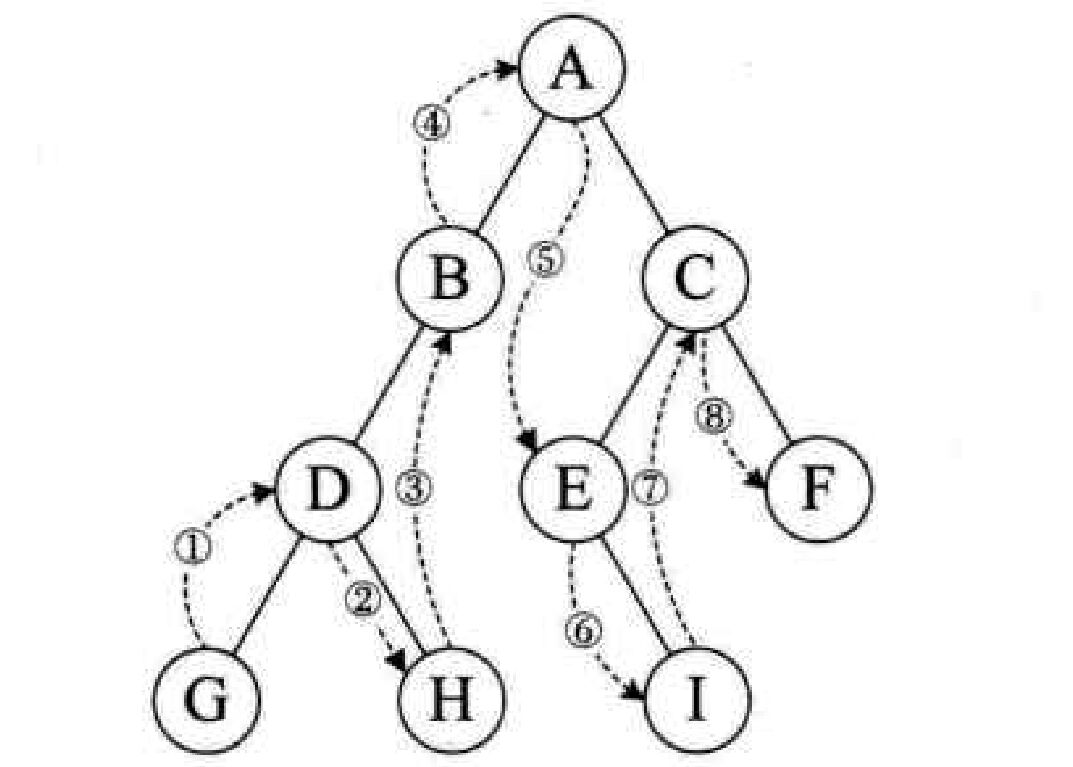
4.3. 中序遍历
[!tip] 以当前节点作为根节点的子树
- 先进入「左子结点」
- 「左子结点」若为
null,则回退「父结点」- 「左边」查询完毕,输出当前结点;然后进入「右子结点」
- 「右子结点」若为
null,则回退「父结点」- 「右子结点」查询完,返回「父结点」
4.4. 后序遍历
[!tip] 以当前节点作为根节点的子树
- 先进入「左子结点」
- 「左子结点」若为
null,则回退「父结点」- 然后进入「右子结点」
- 「右子结点」若为
null,则回退「父结点」- 「右子结点」查询完,输出当前结点值,返回「父结点」
4.5. 层级遍历
[!note|style:flat] 广度优先搜索: 详细代码见「二叉树章节」
4.6. 二叉树的建立
通过「前序和中序」遍历结果构造二叉树:详细代码见「二叉树章节」
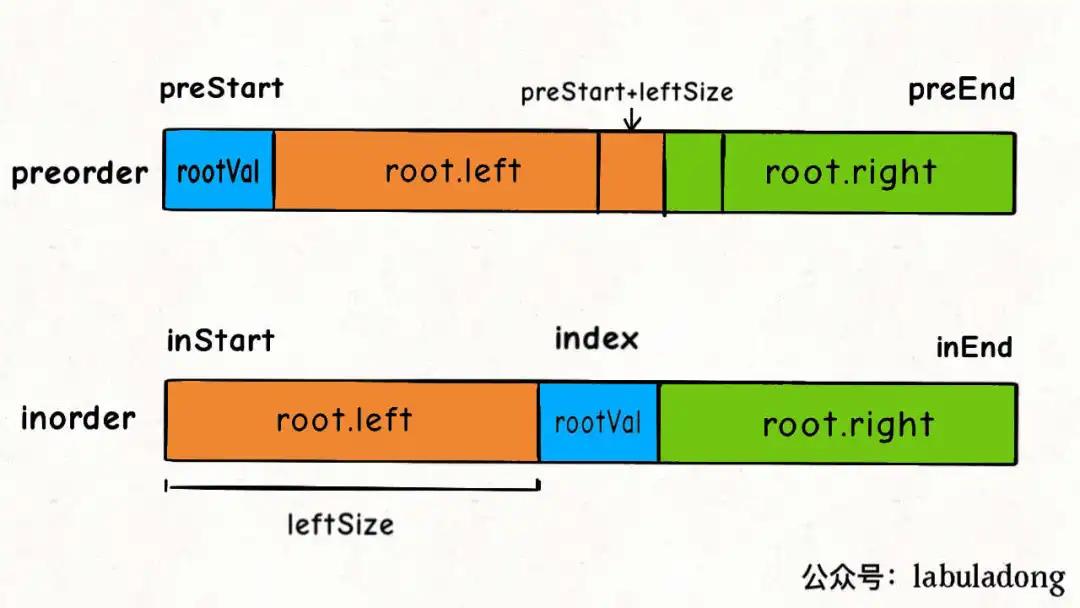
通过「中序和后序」遍历结果构造二叉树:详细代码见「二叉树章节」
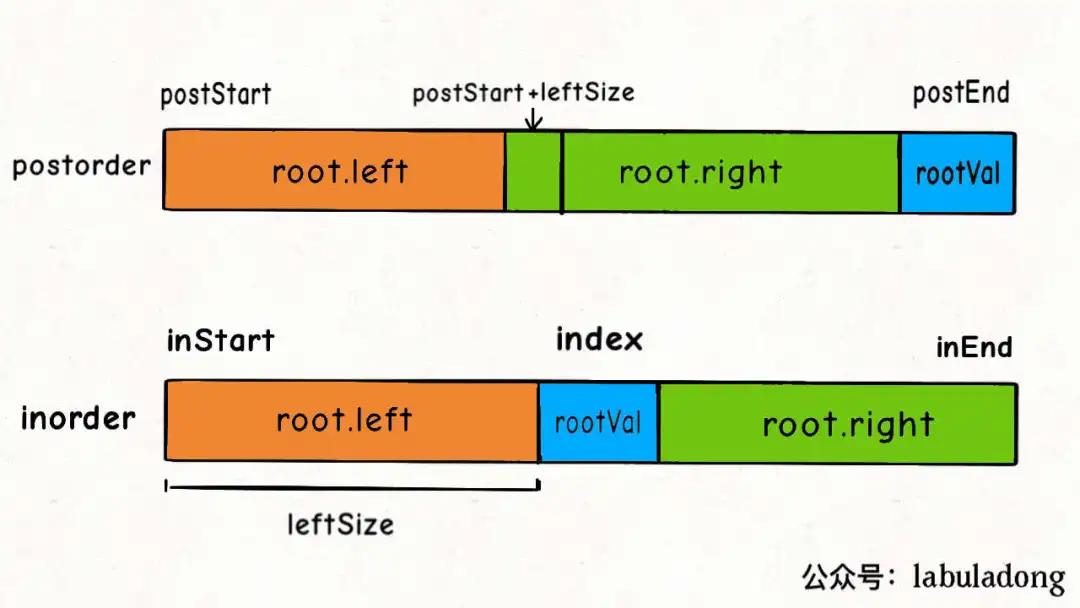
[!tip]
- 先从「前/后序列」结果中找到
rootVal- 然后,再「中序列」结果中找到
rootVal- 根据
rootVal将「中序列」拆成「左,右」两半;根据leftSize位置关系将「前/后序列」拆成「左,右」两半- 「左半」是「左子树」,「右半」是「右子树」;「左、右子树」重复上述步骤,直到所有结点都找完。
5. 二叉查找树 Binary Search Tree
[!note|style:flat]
- 二叉查找树:「根节点」的值大于其左子树中任意一个节点的值,小于其右子树中任意一节点的值,且该规则适用于树中的每一个节点。
- 「中序遍历」为升序
- 二叉查找树的查询效率介于
O(log n) ~ O(n)之间,最大糟糕的查差次数为「二叉树高度」。
class Note
{
public:
int val;
Note *left;
Note *right;
Note(int val) : val(val)
{
left = nullptr;
right = nullptr;
}
~Note()
{
if (left != nullptr)
{
delete left;
}
if (right != nullptr)
{
delete right;
}
}
};
class BinarySearchTree
{
public:
Note *parent;
Note *search(Note *root, int val)
{
// 搜索完毕都没找到:返回 nullptr ;找到了 :返回找到的结点
if (root == nullptr || root->val == val)
{
return root;
}
// 往子结点找
if (root->val < val)
{
parent = root;
return search(root->right, val);
}
else
{
parent = root;
return search(root->left, val);
}
}
// 该数据元素的插入位置一定位于二叉排序树的叶子结点,并且一定是查找失败时访问的最后一个结点的左孩子或者右孩子。
bool insert(Note *root, int val)
{
parent = nullptr;
// 没找到
if (search(root, val) == nullptr)
{
Note *cur = new Note(val);
if (val < parent->val)
{
parent->left = cur;
}
else
{
parent->right = cur;
}
return true;
}
// 找到了,就啥也不干
return false;
}
Note* remove(Note *root, int val)
{
parent = nullptr;
Note *target = search(root, val);
Note* del;
if (target == nullptr)
{
return root;
}
// target 没有左
if (target->left == nullptr)
{
// 当删除点是 根
if(target == root){
root = target->right;
}else{
if(parent->left == target){
parent->left = target->right;
}else{
parent->right = target->right;
}
}
del = target;
}
// target 没有右
else if(target->right == nullptr){
// 当删除点是 根
if(target == root){
root = target->left;
}else{
if(parent->left == target){
parent->left = target->left;
}else{
parent->right = target->left;
}
}
del = target;
}
// 左右都有
else{
Note* sub = target->left;
// 找到 中序 前驱动
while (sub->right != nullptr)
{
parent = sub;
sub = sub->right;
}
target->val = sub->val;
del = sub;
if(parent->left == sub){
parent->left = sub->left;
}
else{
parent->right = sub->left;
}
}
del->left = nullptr;
del->right = nullptr;
delete del;
return root;
}
void sort(Note *root)
{
if (root == nullptr)
{
return;
}
traverse(root->left);
printf("%d \n", root->val);
traverse(root->right);
}
void traverse(Note *root)
{
if (root == nullptr)
{
printf("#\n");
return;
}
printf("%d \n", root->val);
traverse(root->left);
traverse(root->right);
}
};
int main(int argc, char const *argv[])
{
BinarySearchTree bst;
Note *root = new Note(40);
bst.insert(root, 12);
bst.insert(root, 15);
bst.insert(root, 20);
bst.insert(root, 42);
bst.insert(root, 42);
bst.insert(root, 43);
bst.traverse(root);
root = bst.remove(root,40);
bst.traverse(root);
delete root;
return 0;
}
1. 查找
根据二叉搜索树的特点,左右找;最差的查找次数,就是二叉搜索树的高度。
Note *search(Note *root, int val)
{
// 搜索完毕都没找到:返回 nullptr ;找到了 :返回找到的结点
if (root == nullptr || root->val == val)
{
return root;
}
// 往子结点找
if (root->val < val)
{
parent = root;
return search(root->right, val);
}
else
{
parent = root;
return search(root->left, val);
}
}
2. 插入
- 插入位置一定位于二叉排序树的「叶子结点」
- 该「叶子结点」一定是查找失败时访问的最后一个结点
bool insert(Note *root, int val)
{
parent = nullptr;
// 没找到
if (search(root, val) == nullptr)
{
Note *cur = new Note(val);
if (val < parent->val)
{
parent->left = cur;
}
else
{
parent->right = cur;
}
return true;
}
// 找到了,就啥也不干
return false;
}
3. 删除
[!tip] 要删除结点存在四种情况:
- 要删除的结点无孩子结点
- 直接删除该结点;整合到情况
1和2- 要删除的结点只有左孩子结点
- 删除该结点;且使被删除节点的父结点指向被删除节点的左孩子结点
- 要删除的结点只有右孩子结点
- 删除该结点;且使被删除节点的父结点指向被删除节点的右孩子结点
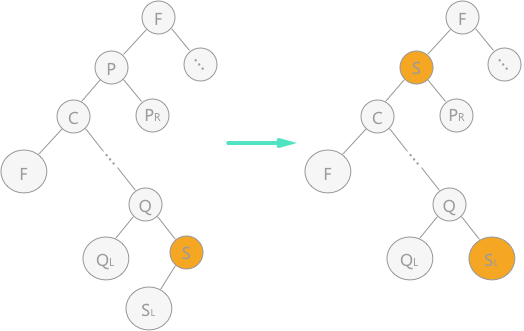
- 要删除的结点有左、右孩子结点
- 见图
- 删除结点为根结点
要删除
p,在对p左子树进行「中序遍历」时,得到的结点p的直接前驱结点为结点s,所以直接用结点s「覆盖」p的值,由于结点s还有左孩子,根据第2条规则,直接将其变为父结点的右孩子。
Note* remove(Note *root, int val)
{
parent = nullptr;
Note *target = search(root, val);
Note* del;
if (target == nullptr)
{
return root;
}
// target 没有左
if (target->left == nullptr)
{
// 当删除点是 根
if(target == root){
root = target->right;
}else{
if(parent->left == target){
parent->left = target->right;
}else{
parent->right = target->right;
}
}
del = target;
}
// target 没有右
else if(target->right == nullptr){
// 当删除点是 根
if(target == root){
root = target->left;
}else{
if(parent->left == target){
parent->left = target->left;
}else{
parent->right = target->left;
}
}
del = target;
}
// 左右都有
else{
Note* sub = target->left;
// 找到 中序 前驱动
while (sub->right != nullptr)
{
parent = sub;
sub = sub->right;
}
// 覆盖
target->val = sub->val;
del = sub;
// 重新组织结构
if(parent->left == sub){
parent->left = sub->left;
}
else{
parent->right = sub->left;
}
}
del->left = nullptr;
del->right = nullptr;
delete del;
return root;
}
6. 平衡二叉搜索树 Balanced binary search trees
参考:
[!note]
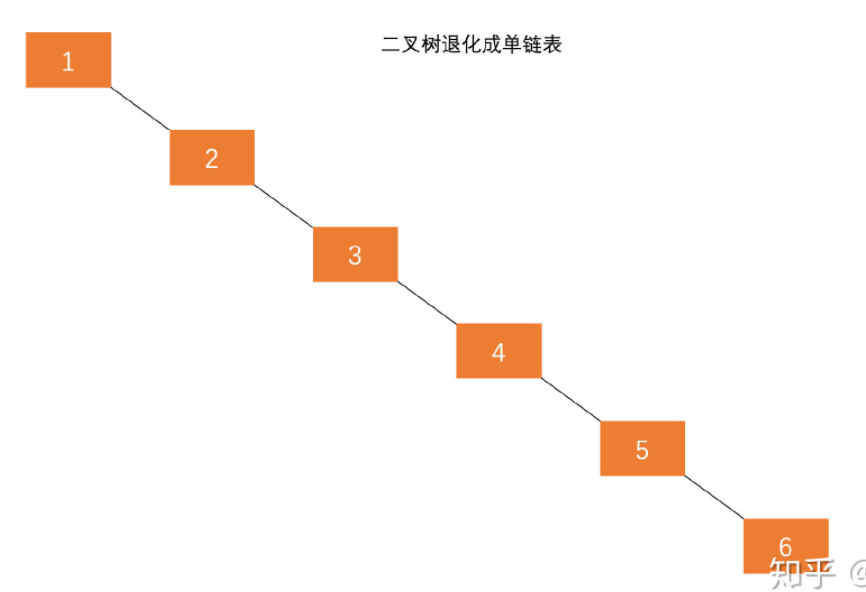
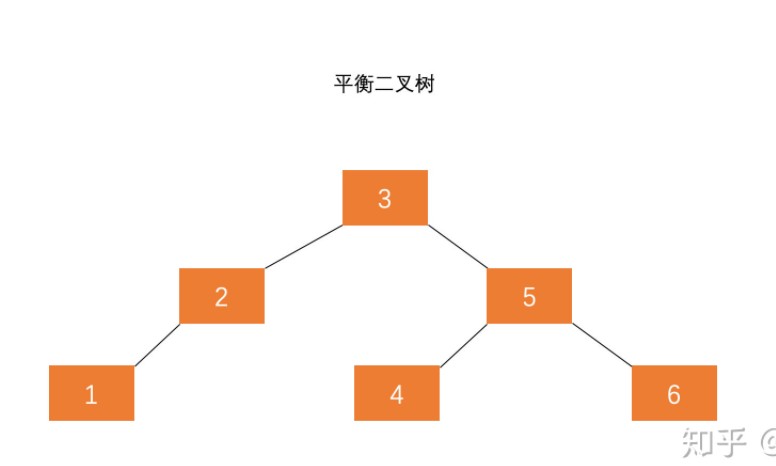
AVL树:「自平衡二叉搜索树」,树中任一节点的两个子树的高度差最大为1,所以它也被称为高度平衡树。由于二叉搜索树添加节点后,可能会朝着某一方向生长,造成二叉树倾斜,二叉树层次增大,导致查找时间边长。平衡二叉搜索树的作用就是通过自身调节,让二叉搜索树平衡生长,层次稳定增长。
- 其查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log n)。
- 一种特殊的「二叉搜索树」
- |平衡因子| 1
6.1. 平衡因子
[!note|style:flat] 一个节点的平衡因子 = 左子树层次 - 右子树层次
6.2. 失衡调整
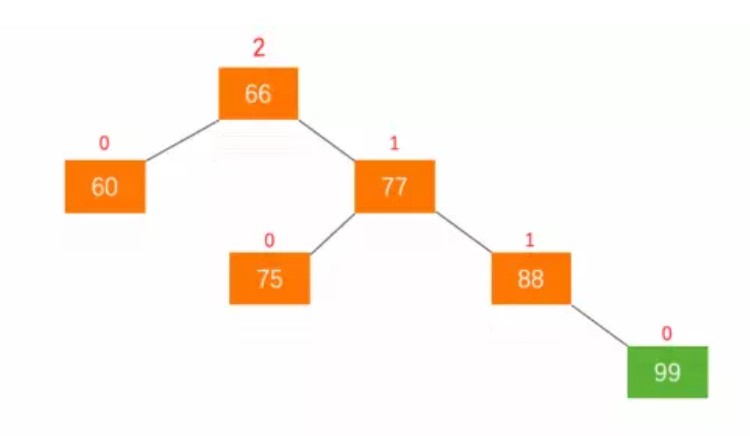
1. 最小失衡子树
定义:在新插入的结点向上查找,以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。下图的最小失衡子树的根结点是66。只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
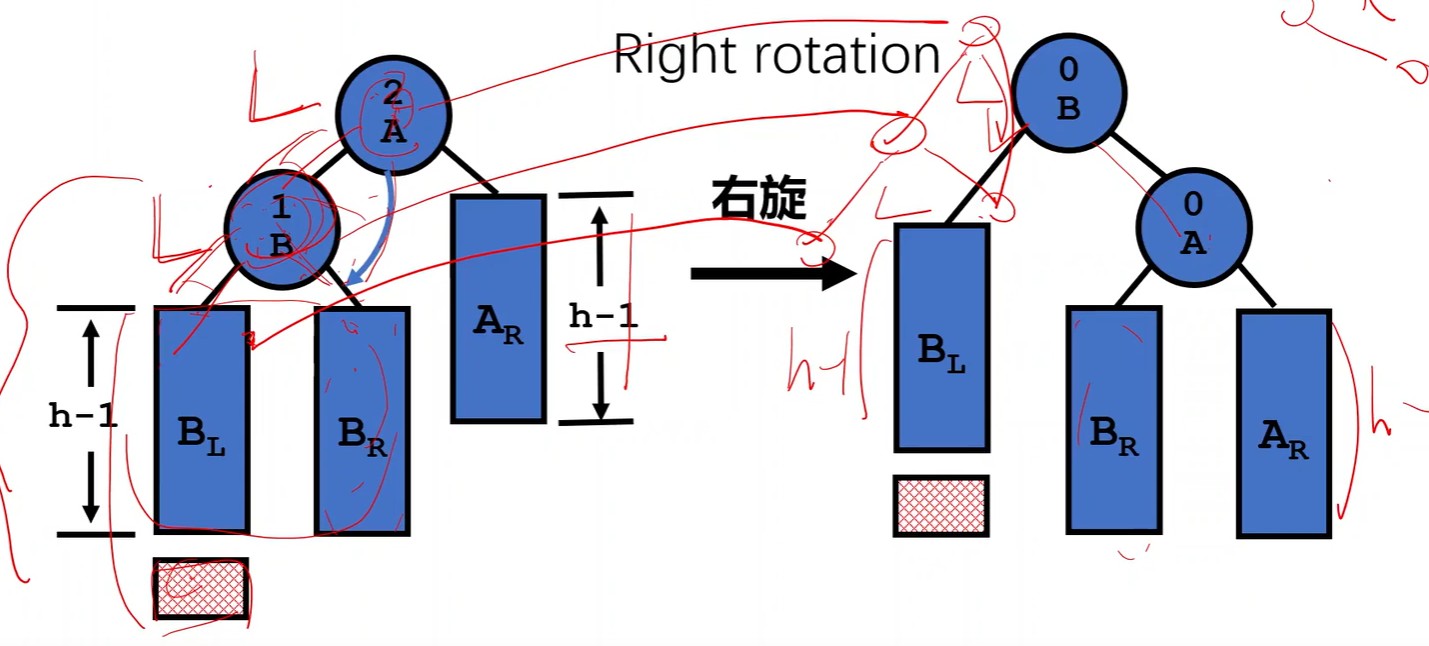
2. LL型
问题:插入的新结点在最小不平衡树的「根结点」的「左孩子」的「左子树」上。
调整:LL型,右旋,右子树变左子树
- 「左孩子
B」变「根结点」, B的「右子树BR」变为「右结点A」的「左子树」
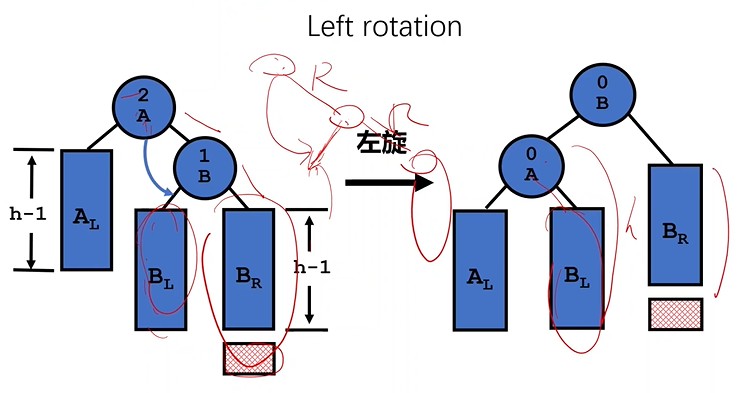
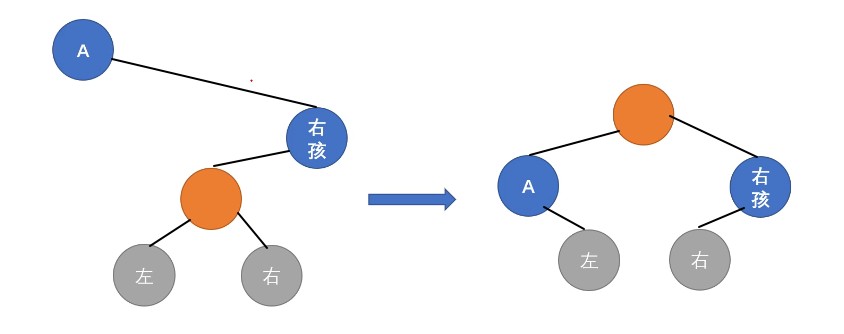
3. RR型
问题:插入的新结点在最小不平衡树的「根结点」的「右孩子」的「右子树」上。
调整:RR型,左旋,左子树变右子树
- 「右孩子
B」变「根结点」, B的「左子树BL」变为「左结点A」的「右子树」
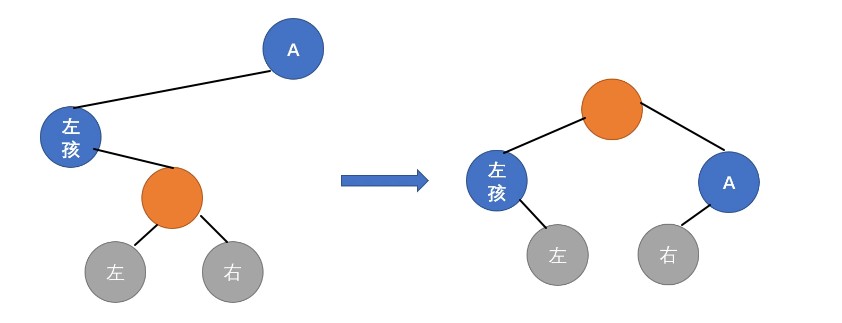
4. LR型
问题:插入的新结点在最小不平衡树的「根结点」的「左孩子」的「右子树」上。
调整:LR型,先左旋,左子树变右子树,再右旋,右子树变左子树
- 「黄结点」变「根结点」,
- 左旋:黄结点与左孩结点,黄结点的「左子树」变为了左孩结点的「右子树」
- 右旋:黄结点与右孩结点,黄结点的「右子树」变为了右孩结点的「左子树」
5. RL型
问题:插入的新结点在最小不平衡树的「根结点」的「右孩子」的「左子树」上。
调整:RL型,先右旋,右子树变左子树,再左旋,左子树变右子树
- 「黄结点」变「根结点」,
- 右旋:黄结点与右孩结点,黄结点的「右子树」变为了右孩结点的「左子树」
- 左旋:黄结点与左孩结点,黄结点的「左子树」变为了左孩结点的「右子树」
7. 2-3-4 树
7.1. 介绍
[!note] 概念: 四阶的「B树(balance tree)」,一种多路查找树
- 所有叶子结点具有同样的深度
- 左孩子结点元素 < 父结点元素 < 右孩子结点元素
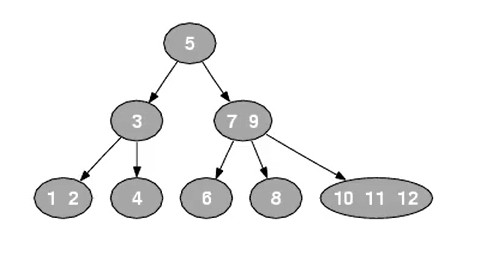
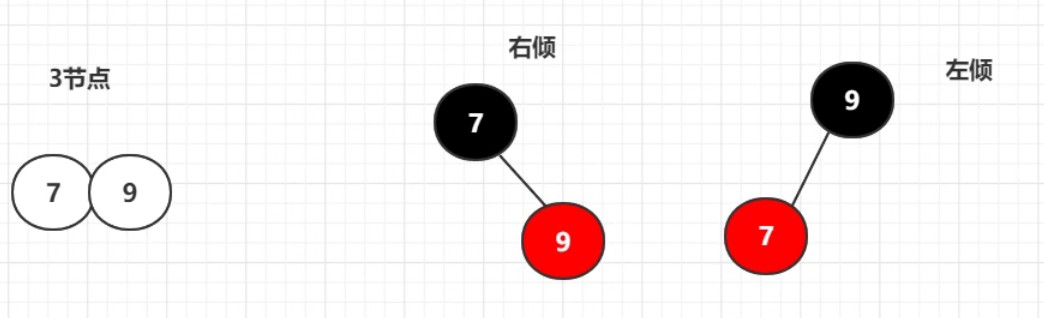
- 2-3-4树包含三种结点
- 2结点:可有2个子结点,1个元素,例如
5、3、4- 3结点:可有3个子结点,2个元素,例如
7 9、1 2- 4结点:可有4个子结点,3个元素,例如
10 11 12生成:2-3-4树的生成
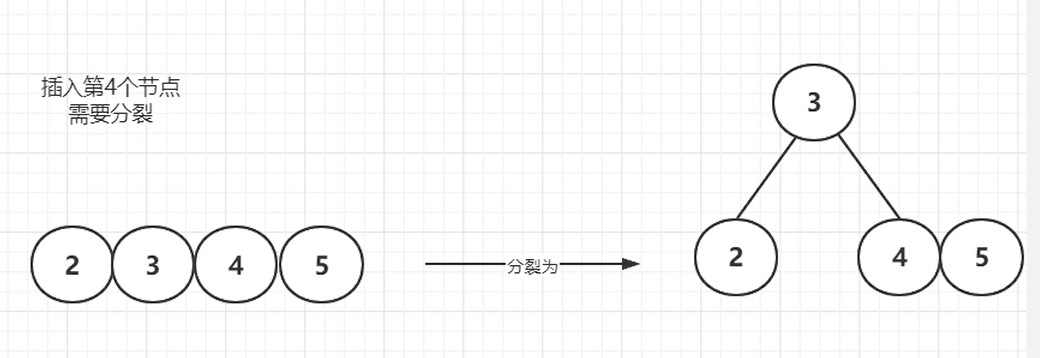
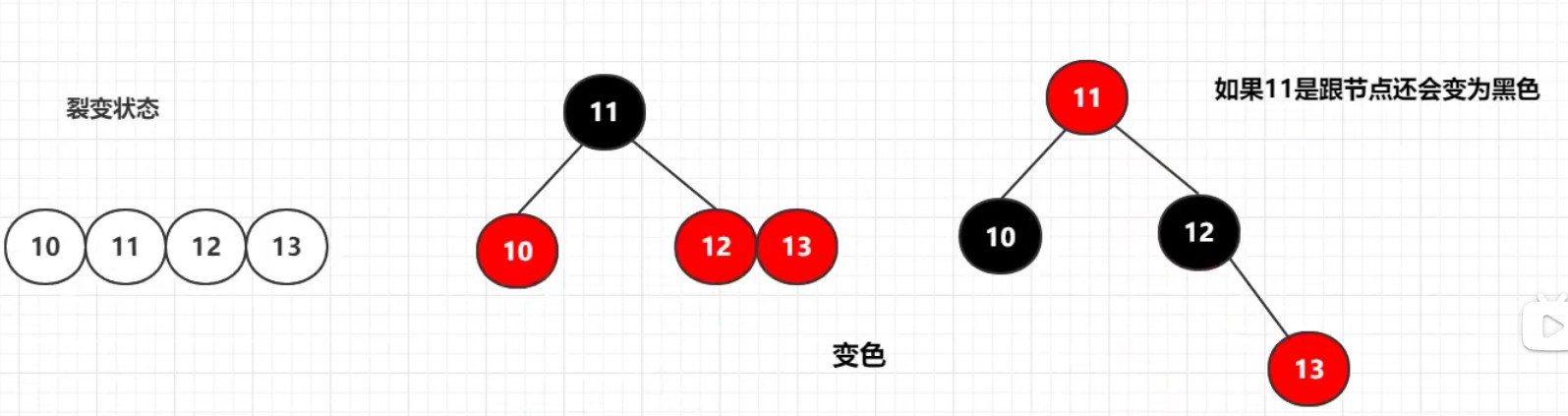
7.2. 分裂
当一个结点由「4」个元素所合并成时,需要对该结点进行分裂。将第二个元素分裂出去作为「父结点」。
7.3. 234树与红黑树的等价关系
8. 红黑树
参考:
8.1. 概念
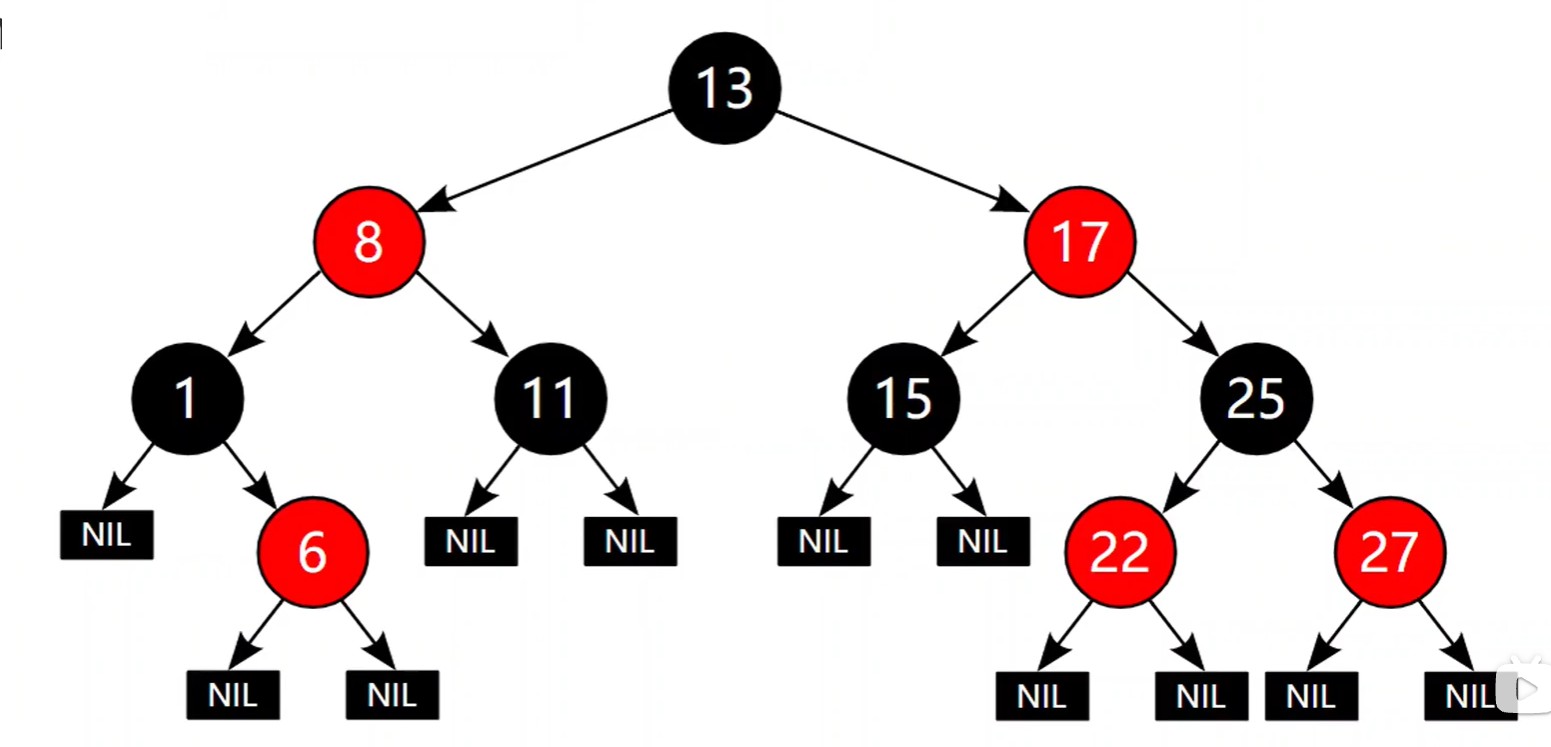
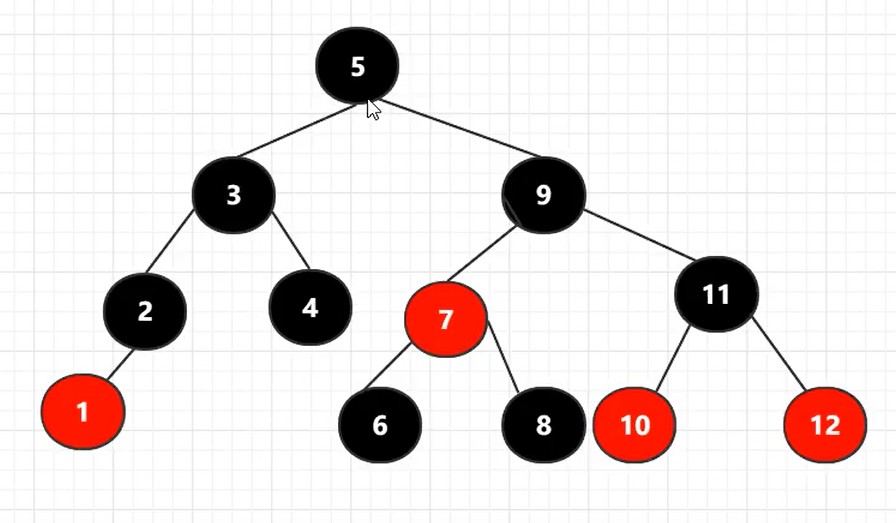
[!note] 作用:红黑树(red-black tree)的产生是由于
AVL的自我结构调整过于频繁,会导致调整的时间可能使用查找的时间还要多,而红黑树的自我调整要求相对于AVL树更松一些。性质:
- 结点要么黑,要么红
- 根结点为黑
NULL被视为叶子结点,且为黑- 两个红色的结点,不能构成父子关系
- 任意一根结点到任意一个叶子结点的路径,所经过的黑色结点个数一样。
9. 二叉堆
[!tip] 采用「完全二叉树」结构进行实现
- 最大二叉堆: 每个节点 >= 子节点
- 最小二叉堆: 每个节点 <= 子节点
10. 生成树和最小生成树
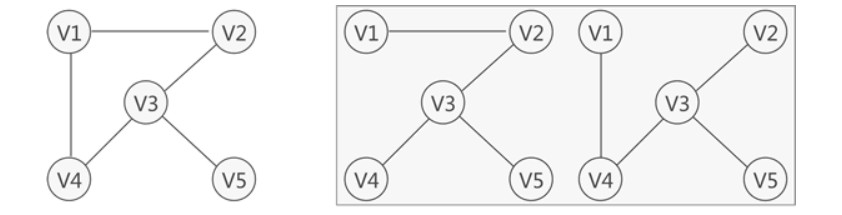
- 生成树: 「连通图」进行遍历(就涉及全部结点),过程中所经过的边和顶点的组合可看做是一棵普通树,通常称为生成树,是原图的一个子图。
- 「连通图」有
n个顶点,生成树有就有n-1条边 - 如果生成树中再添加一条边,则必定成环
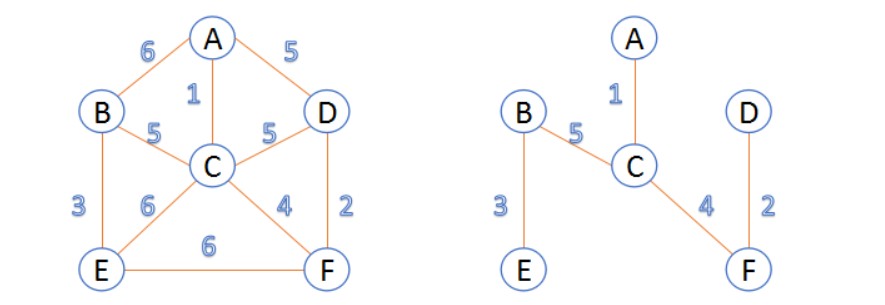
- 「连通图」有
- 最小生成树: 代价和最小的「生成树」,就是边上面的数字和最小。
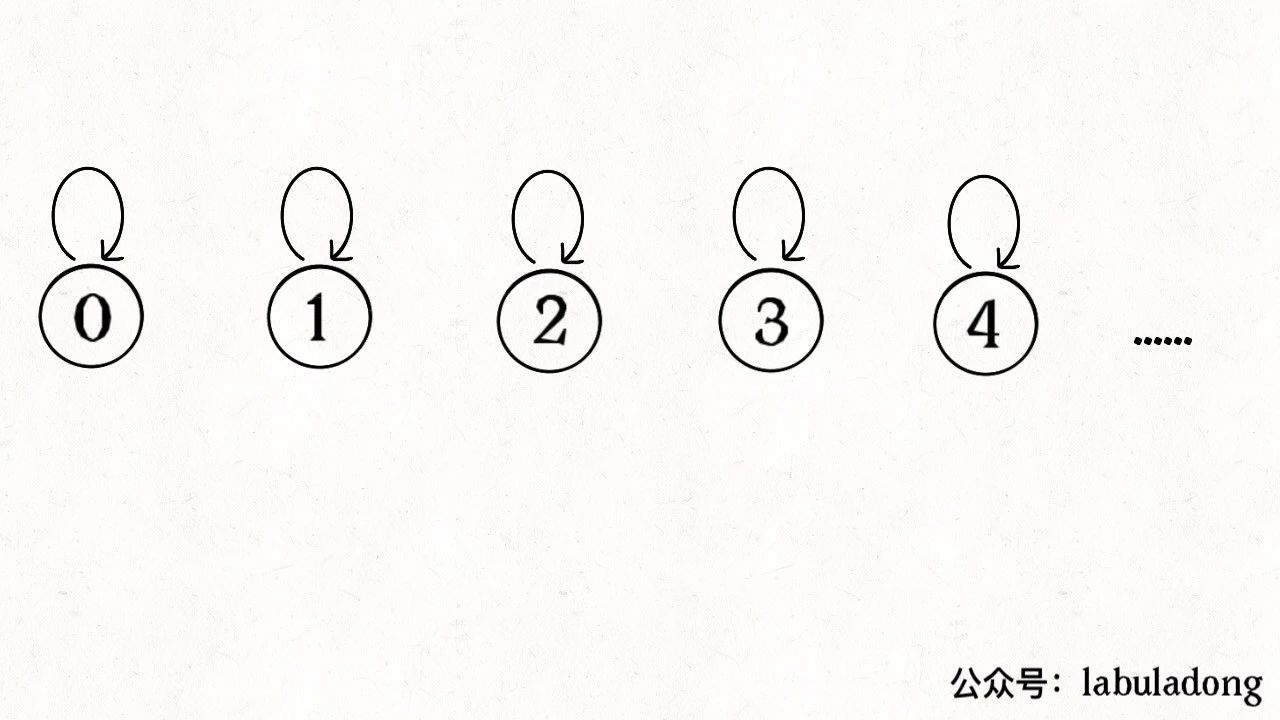
11. 并查集(union_find)
11.1. 概念
[!note|style:flat] 使用前提:
- 一堆独立的元素
- 问题与关于这些元素「能否动态连通」有关,即将问题转为「元素之间连没连通」。「连通」也可以理解为共性,等效。
并查集解题思路:想办法让元素「分门别类」,建立动态连通关系。
class UF {
/* 将 p 和 q 连接 */
public void union(int p, int q);
/* 判断 p 和 q 是否连通 */
public boolean connected(int p, int q);
/* 返回图中有多少个连通分量 */
public int count();
/* 找根 */
public int findRoot(int q);
}
class UnionSet{
public:
vector<int> parents;
vector<int> weights;
// 统计连通分量
int count;
void initialize(int n){
for(int i = 0; i < n;i++){
parents.push_back(i);
weights.push_back(1);
}
count = parents.size();
}
// 查找
int findRoot(int element){
while (element != parents[element])
{
// 把当前父节点跳一级,实现路径压缩
parents[element] = parents[parents[element]];
element = parents[element];
}
return element;
}
void connect(int a,int b){
// 找根
int rootA = findRoot(a);
int rootB = findRoot(b);
if(rootA == rootB){
return;
}
// 增加重量的连接,让树长得更加均匀
if (weights[rootA] > weights[rootB])
{
parents[rootB] = rootA;
weights[rootA] += weights[rootB];
}else{
parents[rootA] = rootB;
weights[rootB] += weights[rootA];
}
count--;
}
bool isConnect(int a,int b){
int rootA = findRoot(a);
int rootB = findRoot(b);
if (rootA == rootB)
{
return true;
}
return false;
}
};
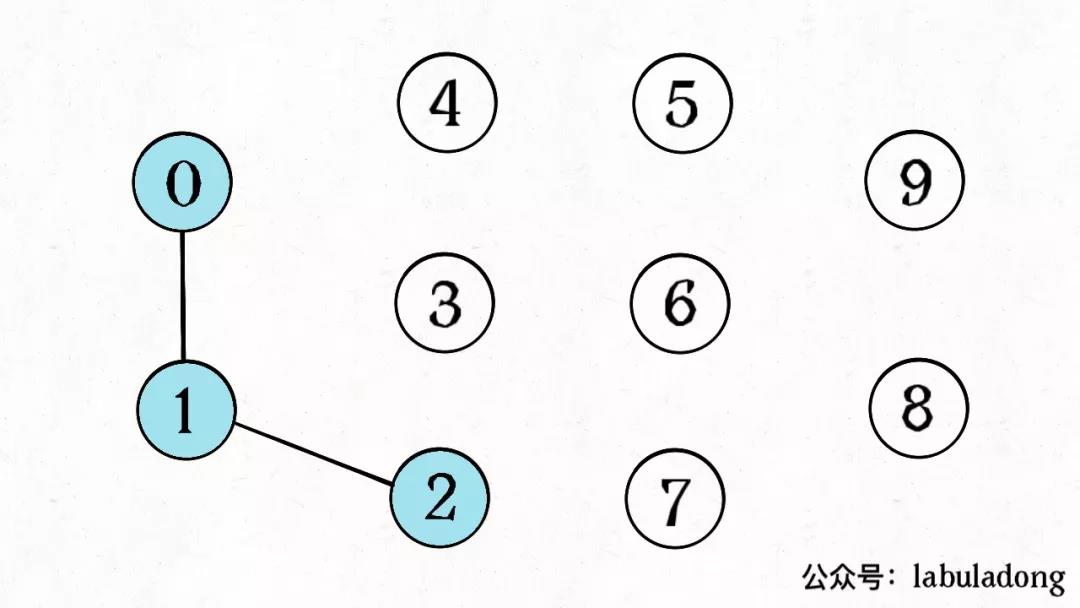
[!note] 并查集:一个集合有多少元素毫不相关;一个集合中的两个元素是否连通。
- 连通分量:集合中毫不相关的元素有多少。比如上图为
8。- 连通:
- 自反:自己和自己连通
- 对称:两个元素互相连通
- 传递:
a与b连通,b与c连通,则c与a之间也是连通的。
11.2. 基本实现
11.2.1. 数据结构
利用一个数组parent[]来储存集合元素,来实现一个图存储:
1)数组的索引为元素值;
2)数组的值为元素的父节点。
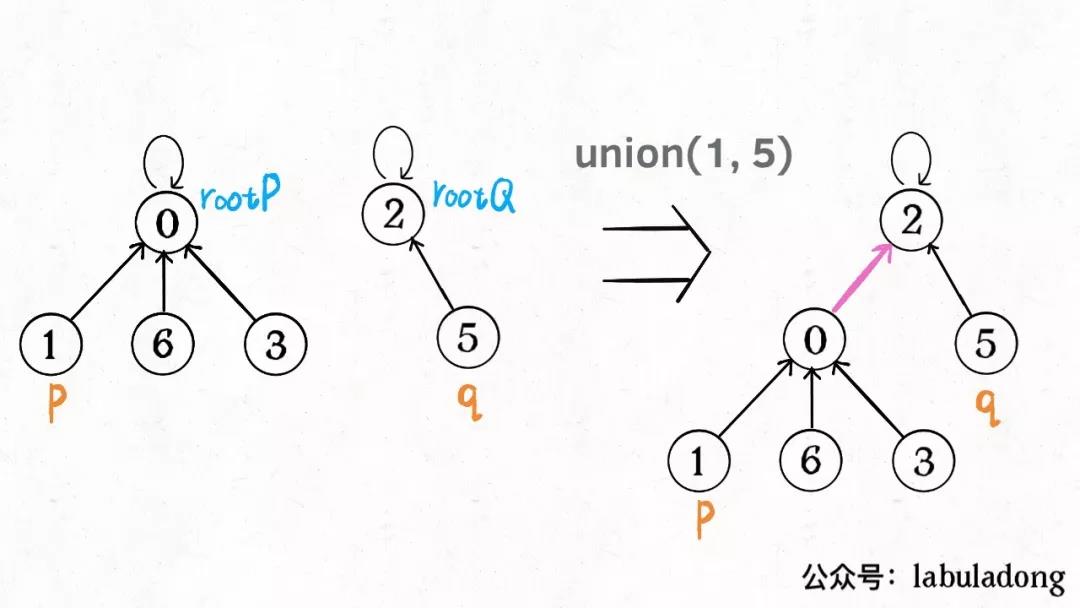
11.2.2. 合并
[!tip]
- 将两个元素遍历到根节点
- 将两个根节点连接起来
11.2.3. 连通
[!tip]
- 将两个元素遍历到各自的根
- 对比根是否一样?连通:不连通
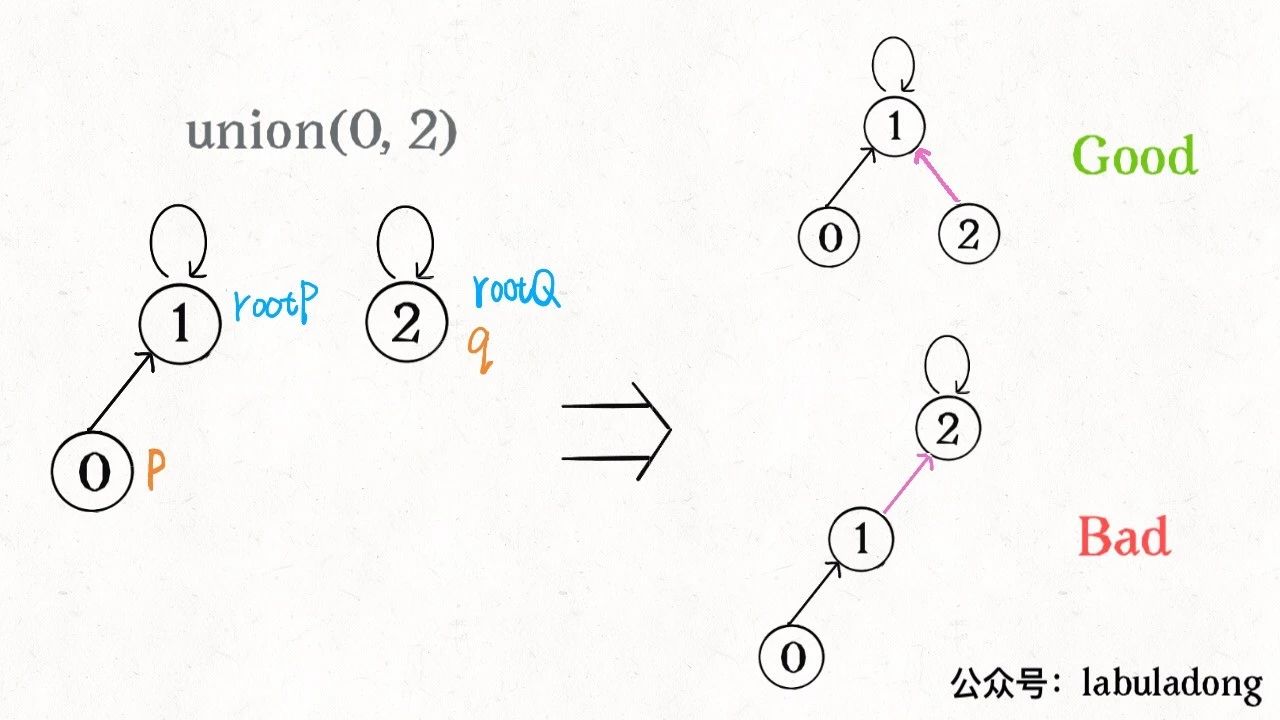
11.3. 平衡性优化
当合并两颗树时,将节点多的一颗树接到轻的树上时,就会造成树的生长不稳定,所以在接树的时候,需要对比两颗树的节点数,少数服从多数。
11.4. 路径压缩(最重要)
[!note|style:flat]
element != parents[element],节点与父节点不一样,就能跳过父节节点,直达爷节点。由于父节点自己指向自己,两个节点时,不会越界。
// 查找
int findRoot(int element){
while (element != parents[element])
{
// 把当前节点的父节点跳一级,实现路径压缩
parents[element] = parents[parents[element]];
element = parents[element];
}
return element;
}
[!tip|style:flat] 压缩路径的优化性能较强与平衡性优化,平衡性优化可以不用写。
11.5. 判定合法算式
题目:
给一组["a==b","b!=c","c==a"]的关系式,判断这些式子能否成立。
==:当成两个元素连通!=: 两个元素不通