回溯算法
1. 框架
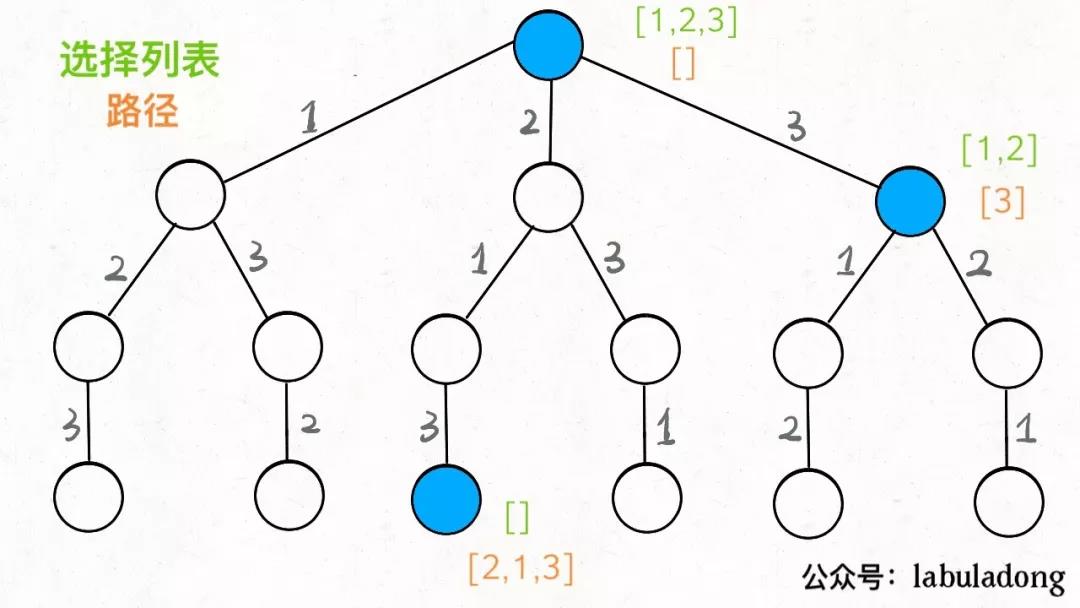
- 路径:记录做过具体的选择
- 标记:标记记录过的选择
- 选择列表:也就是你当前可以做的选择。
- 结束条件:也就是到达决策树底层,无法再做选择的条件。
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」。
2. 全排列
void printAll(const vector<int> & nums,vector<int> &path,vector<int> &book){
// 结束
if(path.size() == nums.size()){
string res = "";
for(int item:path){
res = to_string(item) + res;
}
cout << res << endl;
}
// 列举所有情况
for (int i = 0; i < nums.size(); i++)
{
if (book[i] == false)
{
// 进入
path.push_back(nums[i]);
book[i] = true;
printAll(nums,path,book);
// 出来
path.pop_back();
book[i] = false;
}
}
// 结束
}
3. 全皇后
[!note|style:flat] 都用回溯算法,时间肯定不达标,放心大胆循环列条件。
bool isOk(vector<string> & bord,int row ,int col){
// 检查行
for (int i = 0; i < bord.size(); i++)
{
if(bord[row][i] == 'Q'){
return false;
}
}
// 检查列
for(int i = 0; i < bord.size(); i++){
if(bord[i][col] == 'Q'){
return false;
}
}
int states[4];
states[0] = row - 1 >= 0;
states[1] = row + 1 < bord.size();
states[2] = col - 1 >= 0;
states[3] = col + 1 < bord.size();
// 上角
if (states[0])
{
if (states[2] && bord[row-1][col-1] == 'Q')
{
return false;
}
if (states[3] && bord[row-1][col+1] == 'Q')
{
return false;
}
}
if (states[1])
{
if (states[2] && bord[row+1][col-1] == 'Q')
{
return false;
}
if (states[3] && bord[row+1][col+1] == 'Q')
{
return false;
}
}
return true;
}
void solveNQueens(vector<string> & bord,int count){
if(count == bord.size()){
for(string str:bord){
cout << str << endl;
}
return;
}
for(int i = 0; i < bord.size(); i++){
if(isOk(bord,count,i)){
bord[count][i] = 'Q';
solveNQueens(bord,count+1);
bord[count][i] = '.';
}
}
}