数组链表操作
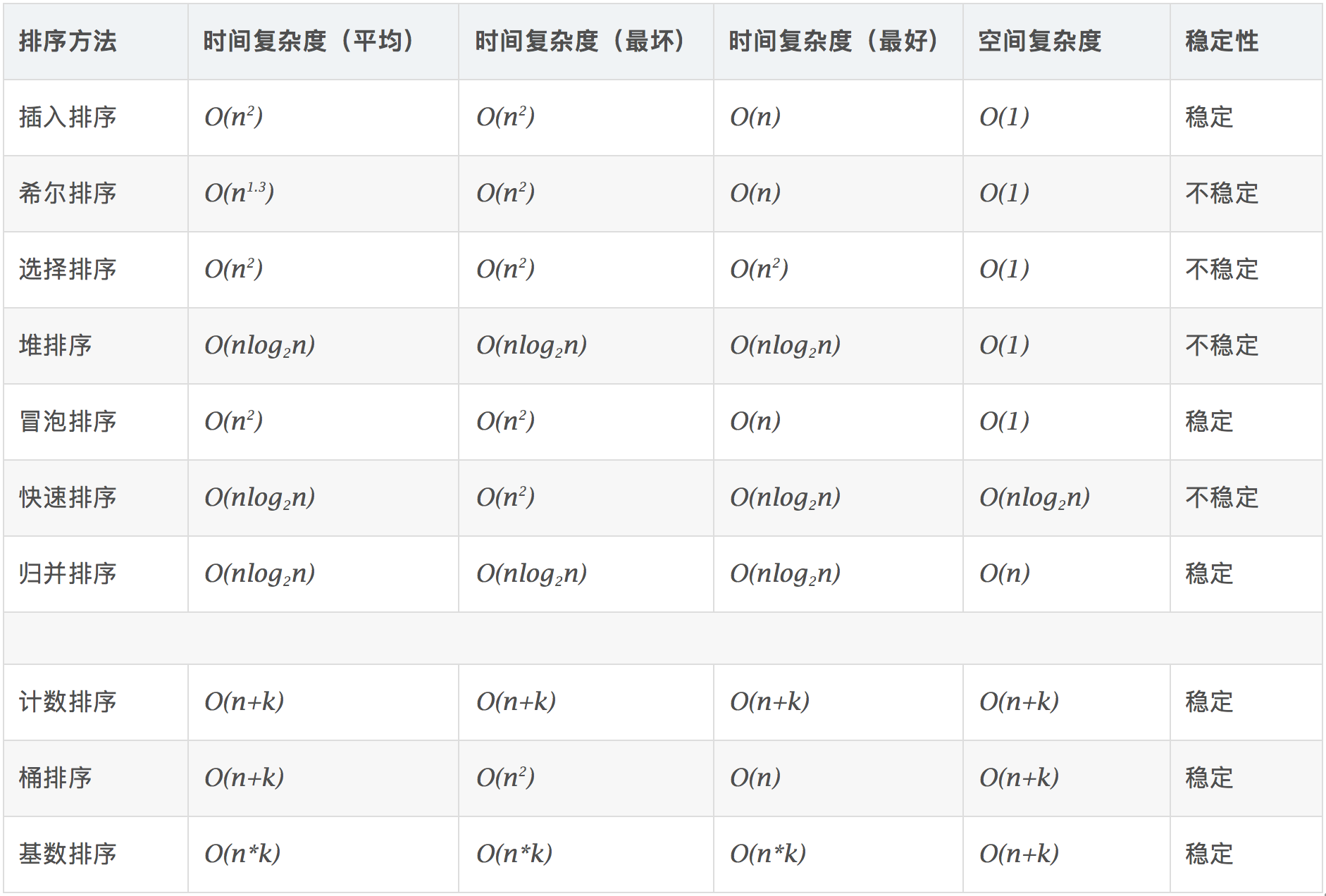
1. 排序
[!tip|style:flat] 稳定的算法:插冒龟,JJ痛。(插入,冒泡,归并,计数,基数,桶)
1.1. 冒泡排序
- 稳定排序,排序之后,数据输入顺序不会乱掉
string str;
for (int i = 0; i < str.size() - 1; i++)
{
for (int j = 0; j < str.size() - i - 1; j++)
{
if (str[j] < str[j+1])
{
char temp = str[j];
str[j] = str[j+1];
str[j+1] = temp;
}
}
}
1.2. 桶排序
- 桶排序可以实现稳定排序
int* in;
// 构建一个桶
vector< vector<int> > bucket(amount,vector<int>());
// 排序
for(int i=0; i < size(in); i++){
bucket[ sortRule(in[i]) ].push_back(in[i]);
}
// 输出
for(int i=0; i < bucket.size();i++){
if(bucket[i].empty()){
continue;
}
for(int j=0; j < bucket[i].size();j++){
bucket[i][j];
}
}
1.3. 快速排序
void quickSort(int left, int right,int* array){
if(left >= right){
return;
}
int l = left;
int r = right;
int base = array[l];
while (l < r)
{
// 移动右边指针,找小于 base 的值
for ( r; r > l ; r --)
{
if (array[r] < base)
{
break;
}
}
// 移动左边指针,找大于 base 的值
for (l; l < r; l++)
{
if (array[l] > base)
{
break;
}
}
// 交换左右值;两指针相遇,就把 base 放到中间
if(l == r){
array[left] = array[l];
array[l] = base;
}else{
int temp = array[l];
array[l] = array[r];
array[r] = temp;
}
}
quickSort(left,l-1,array);
quickSort(l+1,right,array);
}
2. 链表
2.1. 构建链表
- 在头部叠加
void appendNode(int val){
Node* newNode = new Node(val);
if (this->head == NULL)
{
this->last = newNode;
this->head = newNode;
}else{
// 在头部叠加
newNode->next = this->head;
this->head = newNode;
}
size++;
}
- 在尾部增加
void pushNode(int val){
Node *newNode = new Node(val);
if (this->head == NULL)
{
this->head = newNode;
this->last = newNode;
}else{
// 在尾部添加
this->last->next = newNode;
this->last = newNode;
}
size ++;
}
2.2. 逆向
2.2.1. 整体逆向: 靠递归的返回过程,完成反转
ListNode reverse(ListNode head) {
// 深入的终止调节
if (head.next == null) return head;
// 返回的链表的尾节点是 head.next
ListNode last = reverse(head.next);
// 在尾节点增加一个节点
head.next.next = head;
// 断开之前方向的链接
head.next = null;
return last;
}
2.2.2. 从首开始的n个局部逆向
将n+1节点位置储存,通过上面递归进行逆向,最后把 n+1 节点接回去。
ListNode successor = null; // 记录第 n + 1 个节点
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
// 让反转之后的尾节点 head 和后面的节点连起来
head.next = successor;
return last;
}
2.2.3. 对m到n的节点进行逆向:
找到对m-1节点进行记录,然后用上面方法逆向,然后接回去。
// 找到第m个节点,然后返回这个节点
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
return reverseN(head, n);
}
// 前进到反转的起点触发 base case,n也用减 1 ,一会儿反转是按照总长度来的
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}
2.3. 一块一块逆向
- 循环实现: 将当前节点,用头方向增长的方式,重新生成一个链表
void reverse(Node* head){
Node* inverseHead = NULL;
Node* currentNode = head;
Node* temp = NULL;
this->last = currentNode;
while ( currentNode != NULL)
{
// 由于还要用,临时存一下
temp = currentNode->next;
// 将当前的节点组成新的链表,采用头部增长的方式
currentNode->next = inverseHead;
inverseHead = currentNode;
// 更新
currentNode = temp;
}
this->head = inverseHead;
}
- 块逆向: 递归深入拆分块,回退拼接块
reverse(a, b): 翻转的区间为:[a,b)
ListNode reverseKGroup(ListNode head, int k) {
if (head == null) return null;
// 区间 [a, b) 包含 k 个待反转元素
ListNode a, b;
a = b = head;
// 循环完毕后,b已经到了 a+k ,[a,b]中间间隔了 k+1 个节点了
for (int i = 0; i < k; i++) {
// 不足 k 个,不需要反转,base case
if (b == null) return head;
b = b.next;
}
// 进行[a,b)的翻转,a就是尾巴,入栈
ListNode newHead = reverse(a, b);
// 出栈,将前面拆分的块又接回去
a.next = reverseKGroup(b, k);
return newHead;
}
3. 回文
3.1. 字符遍历找回文
string palindrome(string& s, int l, int r) {
// 防止索引越界
while (l >= 0 && r < s.size()
&& s[l] == s[r]) {
// 向两边展开
l--; r++;
}
// l与r在退出循环时,又多算了一次,所以要还原
return s.substr(l + 1, r - l - 1);
}
3.2. 判断链表是否是回文
最简单的办法就是,把原始链表反转存入一条新的链表,然后比较这两条链表是否相同。
// 左侧指针
ListNode left;
boolean isPalindrome(ListNode head) {
left = head;
return traverse(head);
}
boolean traverse(ListNode right) {
if (right == null) return true;
boolean res = traverse(right.next);
// 后序遍历代码
res = res && (right.val == left.val);
left = left.next;
return res;
}
4. 双指针
4.1. 快慢指针
快慢指针一般都初始化指向链表的头结点head,前进时快指针fast在前,慢指针slow在后。
4.1.1. 判定链表中是否含有环
`fast`的移动速度为`slow`的两倍。boolean hasCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) return true;
}
return false;
}
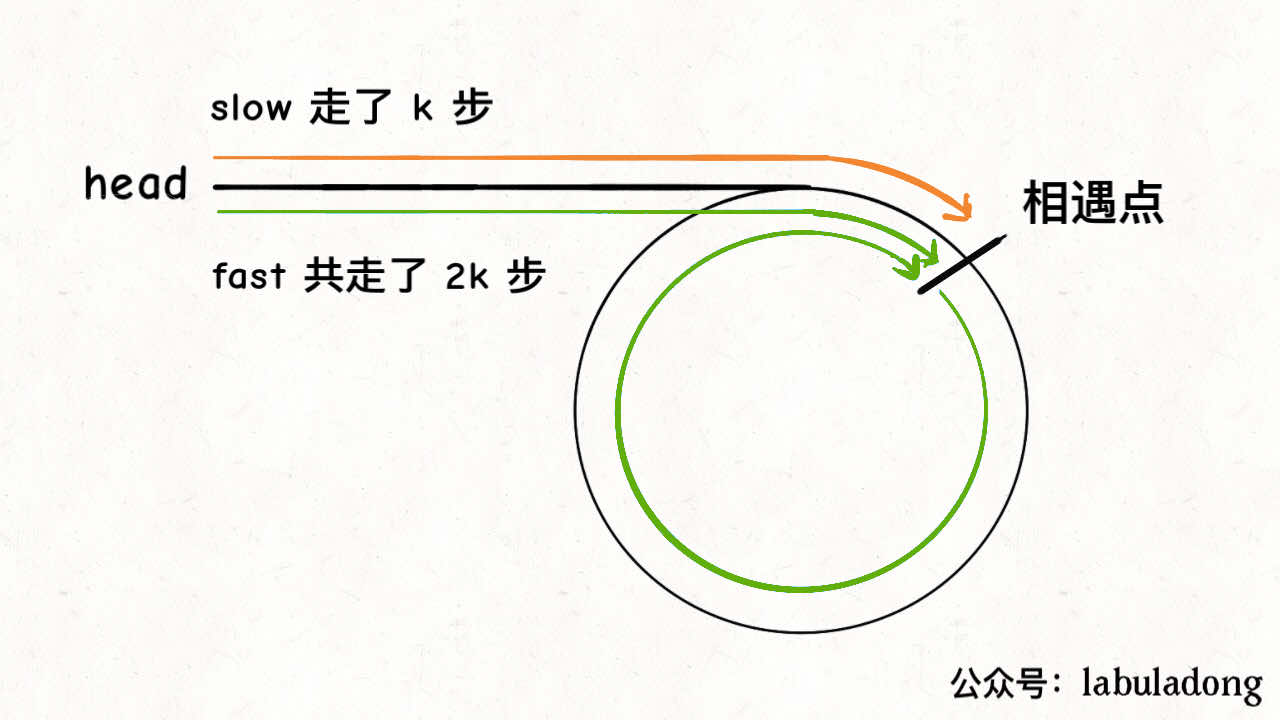
4.1.2. 已知链表中含有环,返回这个环的起始位置
ListNode detectCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;
}
// 上面的代码类似 hasCycle 函数
slow = head;
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
fast一定比slow多走了k步,这多走的k步其实就是fast指针在环里转圈圈,所以k的值就是环长度的「整数倍」。
4.1.3. 链表的中间位置
ListNode middleNode(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
// slow 就在中间位置
return slow;
}
链表的长度是奇数,slow恰巧停在中点位置
链表的长度是偶数,slow最终的位置是中间偏右:
4.1.4. 寻找链表的倒数第n个元素
让快指针先走n步,然后快慢指针开始同速前进;这样当快指针走到链表末尾null时,慢指针所在的位置就是倒数第n个链表节点(n不会超过链表长度)
ListNode removeNthFromEnd(ListNode head, int n) {
ListNode fast, slow;
fast = slow = head;
// 快指针先前进 n 步
while (n-- > 0) {
fast = fast.next;
}
if (fast == null) {
// 如果此时快指针走到头了,
// 说明倒数第 n 个节点就是第一个节点
return head.next;
}
// 让慢指针和快指针同步向前
while (fast != null && fast.next != null) {
fast = fast.next;
slow = slow.next;
}
// slow.next 就是倒数第 n 个节点,删除它
slow.next = slow.next.next;
return head;
4.1.5. 有序数组/链表去重
数组nums[]有顺序,slow走在后面,快指针fast走在前面探路,比较nums[fast]与nums[slow],找到不重复的元素就告诉slow并让slow前进一步。nums[0 slow]便是去重后的数组。
int removeDuplicates(int[] nums) {
if (nums.length == 0) {
return 0;
}
int slow = 0, fast = 0;
while (fast < nums.length) {
if (nums[fast] != nums[slow]) {
slow++;
// 维护 nums[0..slow] 无重复
nums[slow] = nums[fast];
}
fast++;
}
// 数组长度为索引 + 1
return slow + 1;
}
ListNode deleteDuplicates(ListNode head) {
if (head == null) return null;
ListNode slow = head, fast = head;
while (fast != null) {
if (fast.val != slow.val) {
// nums[slow] = nums[fast];
slow.next = fast;
// slow++;
slow = slow.next;
}
// fast++
fast = fast.next;
}
// 断开与后面重复元素的连接
slow.next = null;
return head;
}
注: 由于c++还需要对new的对象进行手动释放,所以可以用数组来储存链表节点,或者使用智能指针。
4.1.6. 删除目标元素,不改变数组顺序
不要求数组有序,如果fast遇到需要去除的元素,则直接跳过,否则就告诉slow指针,并让slow前进一步。nums[0 slow-1]是去除元素后的数组
int removeElement(int[] nums, int val) {
int fast = 0, slow = 0;
while (fast < nums.length) {
if (nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
}
fast++;
}
return slow;
}
4.1.7. 移动零
上一问题的变种
4.2. 左右指针
一般初始化为: left = 0, right = nums.length - 1
- 二分查找
- 翻转数组
- 双指针,升序列,求两数之和
4.2.1. 田忌赛马
struct Entry{
int index;
int val;
Entry(int index, int val) : index(index), val(val){
}
Entry(){}
};
class Compare{
public:
bool operator()(const Entry & A,const Entry & B)const{
if (A.val > B.val)
{
return true;
}
return false;
}
};
void optinalSequence(const int* nums1,int* nums2,int n ){
vector<Entry> target;
vector<int> option;
for (int i = 0; i < n; i++)
{
target.push_back(Entry(i, nums1[i]));
option.push_back(nums2[i]);
}
// 从大到小
sort(target.begin(),target.end(),Compare());
// 从小到大
sort(option.begin(),option.end());
// 左右指针
int left = 0;
int right = n - 1;
for (int i = 0; i < n; i++)
{
// 打得赢
if (option[right] > target[i].val)
{
nums2[target[i].index] = option[right];
right--;
}else{ // 打不赢,就用小的凑数
nums2[target[i].index] = option[left];
left++;
}
}
}
- 凌乱的数组先排序
left: 指向最小的一端right: 指向最大的一段