动态规划

1. 动态规划概念

动态规划问题的一般形式就是求最值。

  • 重叠子问题: 最终点问题是由某一单步小问题的重复，这些 小问题的求解可能会重复计算。
  • 最优子结构: 当前步骤的最优只与"上一步"有关。根据这个特点可以状态压缩
  • 状态转移方程: 递推式，解决问题的核心。

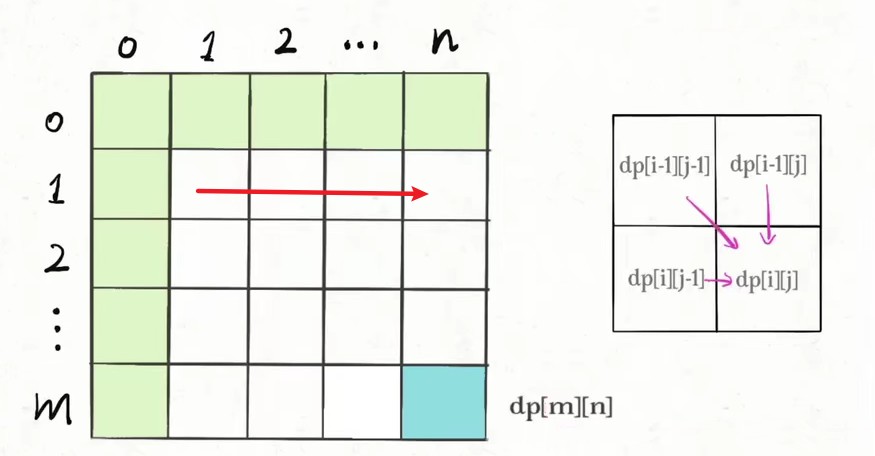
[!note|style:flat] 认为dp[i][j-1]就是问题在状态i,j-1下的结果，dp[i-1][j-1]就是问题在状态i-1,j-1下的结果，其余之前的状态同理。 也就是说，抵达i,j状态之前，dp[][]已经将i,j状态之前的状态全部尝试了一遍，并得到了相应的结果。

1.1. 解题框架

  1. 明确 base case: 如何初始化dp[]；确定边界条件。
  2. 明确「状态」: 推进子问题向大问题演变的变量。就是dp[i]的游标i的含义。
  3. 明确「选择」: 可以使得由过去的状态i-1,i-2,i-3...向当前状态i推进的 「选择」。
  4. 定义 dp 数组/函数: dp值 = f（当前状态）
    • dp函数: 参数就是上面说到的「状态」。函数的返回值就是「结果」。
    • dp[i] 数组：i为「状态」，「结果」为dp[i]
# 初始化
dp[] = init

# 边界条件
dp[0][0][...] = base

# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

1.2. 流程方向

  • 自顶向下: 从目标开始，把大问题拆解小问题，直到到初始条件。
    • 暴力递归: 把大问题拆成小的，递归下去
    • 备忘录递归: 算过的值记录下来，不在重复算
  • 自底向上: 从初始开始，根据递推式，一步一步迭代，直到目标结束。
    • dp数组: 从初始状态，根据递推关系，算到目标状态，循环数组，不用递归。

1.3. 重复子问题的确定

dp[i][j] = min{
        dp[i-1][j] + 1,
        dp[i][i-1] + 1,
        dp[i-1][j-1] + 1
    }

  当从dp[i-1][j-1]过度到dp[i][j]的求解有多种路径时，就存在解重叠的情况。采用备忘录和dp数组解决。

1.4. 状态遍历顺序

dynamic

[!note|style:flat]

  1. 确定二维表dp[][]初始值
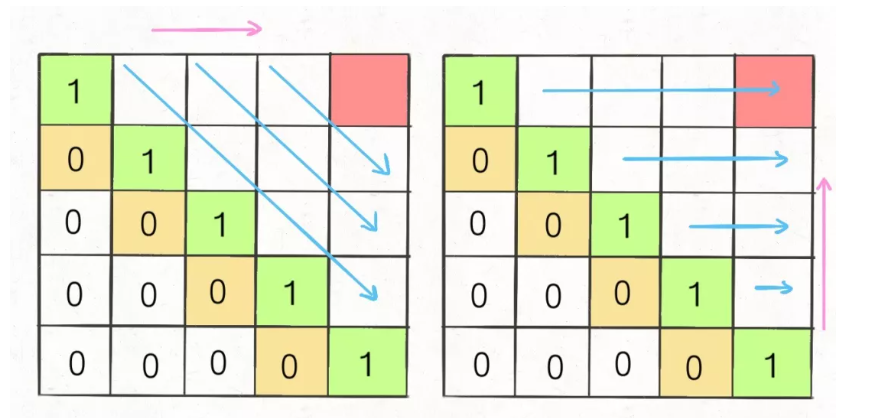
  2. 确定递推式dp[i][j]的依赖情况（上图左边）
  3. 根据依赖关系填充二维表，满足横向填充或者纵向填充
// i = 0, j = 0 的情况是边界条件，已经初始化好了。 
    for (int i = 1; i <= m; i++){
        for (int j = 1; j <= n;j++){
            dp[i][j] = f(dp[i-1][j-1],dp[i][j-1],dp[i-1][j]);
        }
    }

2. 斐波那契级数

题目： 某人有一对兔子饲养在围果它们每个月生1对兔子，且新的兔子在第2个月后(3个月为周期)也是每个月生1对兔子,问一年后围墙中共有多少对兔子。

递推式： f(n)=f(n−1)+f(n−2) f(n) = f(n-1) + f(n - 2) 序列为：1，1，3，5，8，13，21，34，55，89。。。

3. 凑零钱问题

题目： 给你k种面值的硬币，面值分别为c1, c2 ... ck，每种硬币的数量无限，再给一个总金额amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1。

分析：

[!tip]

  • 状态： amount 能推荐问题递推，问题的结果由amount影响
  • 选择： 每次「状态」的推进，由c1, c2 ... ck确定。
  • dp[amount]定义：dp[amount]表示，当总金额为amount时，最少硬币数为dp[aomunt]
实现代码
int coinChange(const int * coins,int n,int amount){

    // 定义dp[i]: 状态为钱总数；结果为当前总价最少钱币数
    // 初始化放入极端值,由于是求解最小，所以放入一个大值
    vector<int> dp(amount + 1,amount + 1);

    // 边界条件
    dp[0] = 0;

    for(int i=2;i <= amount ; i++){
        // 选择当前的货币
        for(int j=0;j < n;j++){
            if(i >= coins[j]){
                dp[i] = min(dp[i],dp[i - coins[j]] + 1);
            }
        }
    } 

    // 找不到
    if (dp[amount] == amount + 1)
    {
        return -1;
    }

    return dp[amount];
}

4. 子序列问题

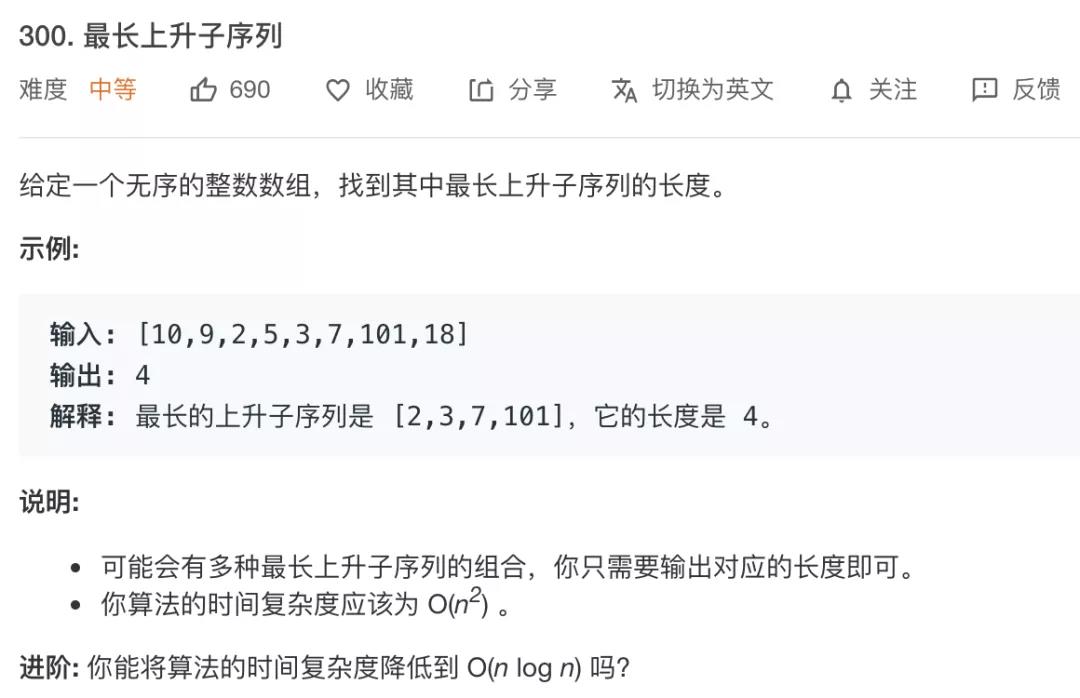
4.1. 最长递增(递减)子序列

undefined

问题特征：

[!note|style:flat]

  • 首先给一组1维的长序列， 若是2维问题，看看能不能排序降为1维问题。
  • 要求子序列具有「某种单调关系」
  • 目标子序列是关系下的「最长子序列」

分析：

[!tip]

  • 状态： 当前查找的序列的以索引i结束
  • 选择： 选择dp[i-1],dp[i-2]...确定dp[i]。
  • dp[i]定义： 以索引i结束的序列，最长子序列的长度dp[i]
实现代码
int lengthOfLIS(vector<int>& seq){

    vector<int> dp(seq.size(),1);

    dp[0] = 1;
    // 状态从 1 索引开始
    for(int i=1;i<seq.size();i++){

        for(int j=0; j < i; j++){
            if(seq[i] > seq[j]){
                dp[i] = max(dp[i],dp[j] + 1);
            }
        } 
    }

    int max = 1;
    for(int item:dp){
        if(item > max) max = item;
    }

    return max;
}

4.2. 信封嵌套问题

undefined

4.2.1. 降维

undefined

[!note|style:flat] 嵌套问题是要求[w,h]「两个」数据均有「单调的大小」关系，属于2维问题。而递增子序列问题是1维问题。 将「2维问题」转「1维问题」可以使用「排序」，先确定一个维度的关系，然后就只用关心一个维度。
排序：对于[v1,v2]形式，一般优先v1升序，若v1相等，则v2降序


4.2.2. 问题求解

[!tip]

  • 排序 : 保证对1维序列进行操作，两点（[v1，v2]）数据，先排序：v1升序，v2降序
  • 状态： 当前查找的序列的以索引i结束
  • 选择： 选择dp[i-1],dp[i-2]...确定dp[i]。
  • dp[i]定义： 以索引i结束的序列，最长子序列的长度dp[i]
实现代码
struct Envelope
{
    int width;
    int height;

    bool greatThan(const Envelope& temp){
        if (this->width > temp.width && this->height > temp.height)
        {
            return true;
        }
        return false; 
    }
};

int maxEnvelopeLen(vector<Envelope> &envelopes){

    // width 升序，hight 降序
    sort(envelopes.begin(), envelopes.end(),[](const Envelope & A, const Envelope & B)->bool{
        if (A.width < B.width)
        {
            return true;
        }else if(A.width == B.width){
            if(A.height > B.height){
                return true;
            }
        }
        return false;
    });

    vector<int> dp(envelopes.size(),1);

    for(int i=0;i<envelopes.size();i++){
        // 选择
        for(int j=0;j<i;j++){

            if (envelopes[i].greatThan(envelopes[j]))
            {
                dp[i] = max(dp[i],dp[j] + 1);
            }
        }
    }

    int max = 0;
    for(int item:dp){
        if (max < item)
        {
            max = item;
        }
    }

    return max; 
}

4.3. 最小编辑距离

undefined

[!tip]

  • 状态： 解决两个字符串的动态规划问题，一般都是用「两个指针」，即「两个状态」。 源头字符串的前j个字符，目标字符串的前i个字符。
  • 选择： 删除，插入，替换，跳过
  • dp[i][j]定义： 目标字符串的前i个字符变为源头字符串的前j个字符，所做的小操作距离

插入： 目标字符串前i个字符与源字符串的前j-1个字符相同的情况，变当前状态i,j dp[i][j]=dp[i][j−1]+1 dp[i][j] = dp[i][j-1] + 1

undefined

删除： 目标字符串前i-1个字符与源字符串的前j个字符相同的情况，变当前状态i,j dp[i][j]=dp[i−1][j]+1; dp[i][j] = dp[i-1][j] + 1;

undefined

替换： 目标字符串前i-1个字符与源字符串的前j-1个字符相同的情况，变当前状态i,j

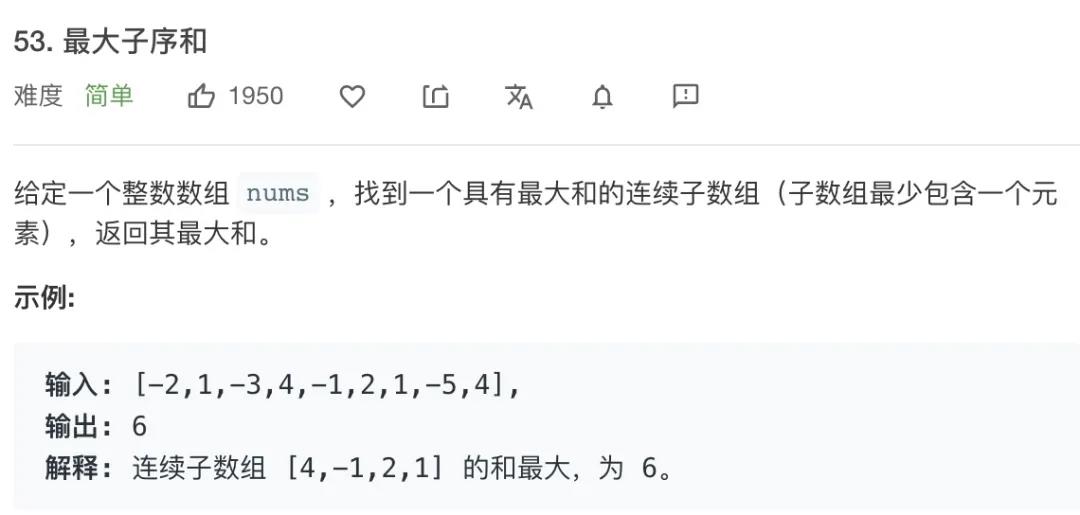
undefined

dp[i][j]=dp[i−1][j−1]+1; dp[i][j] = dp[i-1][j-1] + 1; > [!warning|style:flat] > **动态规划状态的迁移：永远是之前已经得出结论的状态，迁移到当前状态；根据`1.4`的状态遍历，之前的状态默认是已经提前都计算好，不必深究。**
代码实现
```cpp int minDistance(const string & S,const string & T){ // 在S的j位置，在T的i位置时，操作数最小 vector< vector > dp(T.length()+1,vector(S.length()+1,0)); // 初始化，当目标是空串时 for(int i=1;i<=s.size();i++){ dp[0][i]="i;" } 初始化，当源是空串时 for(int i="1;i<=T.length();i++){" dp[i][0]="i;" for (int j="1;" <="S.length();" j++) { if (t[i-1]="=" s[j-1]) dp[i][j]="dp[i-1][j-1];" }else{ 替换 + 1; 删除 1); 插入 return dp[t.length()][s.length()]; ```
## 4.4. 最大子数组之和

undefined

[!tip]

  • 状态： 数组的当前索引i
  • 选择： 由于是「连续子数组」，那就只能和挨着的对比，即dp[i],dp[i-1]
  • dp[i]定义： 以nums[i]为结尾的「最大子数组和」为dp[i]
实现源码
int maxSum(vector<int> &nums){

    // 初始化
    vector<int> dp(nums);

    for (int i = 1; i < nums.size(); i++)
    {
        dp[i] = max(dp[i],dp[i-1] + nums[i]);
    }

    sort(dp.begin(),dp.end());

    return dp[dp.size()-1];
}

4.5. 最长公共子序列问题

4.5.1. 算法

问题： 输入s1 = "zabcde", s2 = "acez"，它俩的最长公共子序列是lcs = "ace"，长度为 3，所以算法返回 3。

[!tip]

  • 状态： 解决两个字符串的动态规划问题，一般都是用「两个指针」，即「两个状态」。 s1的前i个字符，s2的前j个字符。
  • 选择： 当s1[i]==s2[j]时，dp[i-1][j-1] + 1；当s1[i]!=s2[j]时，要找一个目前最大子串长度值max(dp[i-1][j],dp[i][j-1])（有可能s1[i]子序列中，有可能s2[j]子序列中）
  • dp[i][j]定义： 在s1的前i个字符，s2的前j个字符时，最大子序列的最大长度。
源码实现
int maxPublicSub(const string& strA,const string& strB){

    vector< vector<int> > dp(strB.size()+1,vector<int>(strA.size()+1,0));


    for (int i = 1; i <= strB.size(); i++)
    {
        for (int j = 1; j <= strA.size(); j++)
        {
            if ( strA[j-1] == strB[i-1])
            {
                dp[i][j] = dp[i-1][j-1] + 1;
            }else{
                dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        }
    }

    return dp[strB.size()][strA.size()];
}

4.5.2. 字符串的删除操作

undefined

4.5.3. 最小 ASCII 删除和

undefined

[!tip]

  • 状态： 解决两个字符串的动态规划问题，一般都是用「两个指针」，即「两个状态」。 s1的前i个字符，s2的前j个字符。
  • 选择： 当s1[i]==s2[j]时，最小的是dp[i-1][j-1]；当s1[i]!=s2[j]时，要删除一个min(dp[i-1][j] + (int)strB[i-1],dp[i][j-1] + (int)strA[j-1])（有可能s1[i]在子序列中，有可能s2[j]在子序列中）
  • dp[i][j]定义： 在s1的前i个字符，s2的前j个字符时，被删除的ascii码最小。
实现代码
int minDeleteASCII(const string& strA,const string& strB){

    vector< vector<int> > dp(strB.size()+1,vector<int>(strA.size()+1,0));

    // 当strA为空时
    for (int i = 1; i <= strB.size(); i++)
    {
        dp[i][0] = dp[i-1][0] + (int)strB[i-1]; 
    }

    // 当strB为空时
    for (int i = 1; i <= strA.size(); i++)
    {
        dp[0][i] = dp[0][i-1] + (int)strA[i-1]; 
    }

    for (int i = 1; i <= strB.size(); i++)
    {
        for (int j = 1; j <= strA.size(); j++)
        {
            if ( strA[j-1] == strB[i-1])
            {
                dp[i][j] = dp[i-1][j-1];
            }else{
                dp[i][j] = min(dp[i-1][j] + (int)strB[i-1],dp[i][j-1] + (int)strA[j-1]);
            }
        }
    }

    return dp[strB.size()][strA.size()];
}

4.6. 子序列/子串问题总结

[!note|style:flat]

  • 子串：
    • dp[i]的定义，一般为 「以i结尾的连续子串。。。。」
  • 子序列：
    • dp[i]的定义，一般为 「从0到i位/置的子串。。。。」
  • 涉及两个字符串/数组时，要用双状态
  • 特例：一个数组，双指针
  • 通过排序，可也把[v1,v2]转为子序列问题。

4.7. 特例：最长子序列回文

undefined

[!tip]

  • 状态： i到j的子串。
  • 选择： 当s1[i]==s1[j]时，增加两个dp[i][j] = dp[i+1][j-1] + 2;；当s1[i]!=s1[j]时，有一个可能在回文里，找最大的dp[i][j] = max(dp[i+1][j],dp[i][j-1]);（有可能s1[i]在子序列中，有可能s1[j]在子序列）
  • dp[i][j]定义： i到j的子串，最大回文数为dp[i][j]。
  • 初始： dp[][]的下半部不会涉及到，所以为0；当i==j时，dp[i][j]=1。

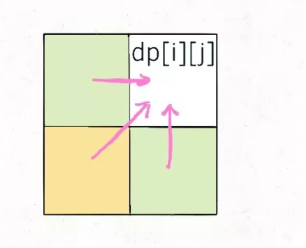
undefined undefined

[!note|style:flat] 由于dp[i][j]与dp[i+1][j-1],dp[i+1][j],dp[i][j-1]有关，所以要重新设置遍历顺序。

代码实现
int maxLenMirror(const string &str){

    vector< vector<int> > dp(str.length(),vector<int>(str.length(),0));

    // 初始化
    for (int i = 0; i < str.length(); i++)
    {
        dp[i][i] = 1;
    }

    for (int i = str.length() - 2; i>=0; i--)
    {
        for (int j = i + 1; j < str.length(); j++)
        {
            if(str[i] == str[j]){
                dp[i][j] = dp[i+1][j-1] + 2;
            }else {
                dp[i][j] = max(dp[i+1][j],dp[i][j-1l]);
            }
        }
    }

    return dp[0][dp.size()-1];
}

results matching ""

    No results matching ""