傅里叶变换,离散傅里叶和快速傅里叶
对于三角函数系:
{1,sinx,cosx,⋯,sinnx,cosnx}(1.1)
任意取两个三角函数,满足:
∫−ππsinnxcosmxdx=0,m=n(1.2)
f(x)可以转换为三角函数系的加和:
f(x)=2a0+k=1∑∞akcoskωx+k=1∑∞aksinkωx(1.3)
函数f(x)周期为T,在复数域下求解得:
f(x)=f(x+T)f(x)=∑−∞∞cneinωxcn=T1∫0Tf(x)e−inωxdx(2.1)
注意:这里的ω=T2π,为基频率,是常值。
函数f(x)没有周期。
f(x)=∫−∞∞c(ω)eiωxdωc(ω)=2π1∫−∞∞f(x)e−iωxdx(3.1)
注意:这里的ω是连续变量。
存在条件:
∫−∞∞∣f(t)∣dt<∞(3.2)
不是新的理论,而是计算cn算法:通过N个离散的等距的采样点,计算出周期为T的函数f(x)的傅里叶级数cn。(这里的 T 可以推广到无周期)
f(x)的傅里叶级数形式为有限个[c0,c1,⋯,cN−1]。
1,定义
wk=ekN2πi(4.1)
2,性质
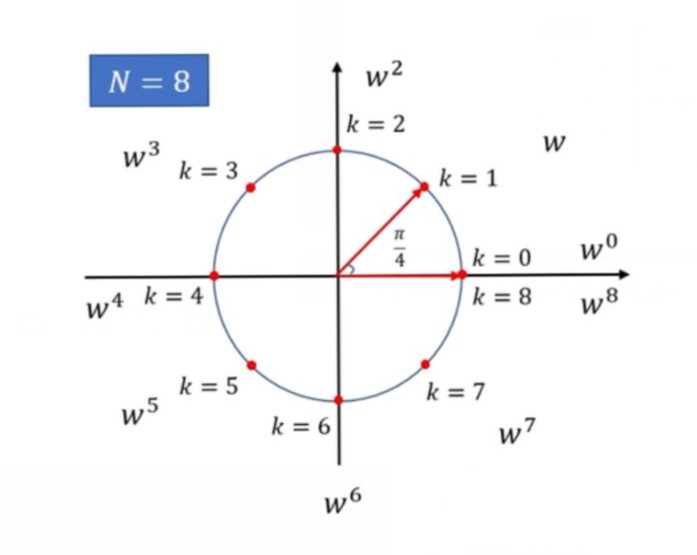
N个采样点,w0,w1,⋯,wN−1,在复平面上是一个圆。对于wN,wN+1,⋯则在这个圆上循环。
取N个采样点[(0NT,f(0NT)),(1NT,f(1NT)),⋯,((N−1)NT,f((N−1)NT))]。分别带入傅里叶级数(2.1),得到N个方程,然后求解方程组,得到cn序列,实现傅里叶变换。
例如,令x=NT,则ωNT=N2π,带入(2.1)得到:
f(NT)=⋯+c−1e−1N2πi+c0e0N2πi+c1eN2πi⋯cNeNN2πi+cN+1e(N+1)N2πi⋯=⋯+c−1w−1+c0w0+c1w1⋯cNwN+cN+1wN+1⋯(4.2)
由所有的wk都可以化解为[w0,w1,⋯,wN−1]中的某个形式。所以(4.2)进一步化解:
f(NT)=(⋯c−N+c0+cN⋯)w0+(⋯c−N+1+c1+cN+1⋯)w1+(⋯c−N+2+c2+cN+2⋯)w2⋯+(⋯c−1+cN−1+c2N−1⋯)wN−1(4.3)
通过(2.1)式还可以看出,x=kNT只会影响f(x)中的wk项,而不会影响cn值。剩余的N-1个采样点均可以按照上述方式进行处理。
f(kNT)=(⋯c−N+c0+cN⋯)w0k+(⋯c−N+1+c1+cN+1⋯)w1k+(⋯c−N+2+c2+cN+2⋯)w2k⋯+(⋯c−1+cN−1+c2N−1⋯)w(N−1)k(4.4)
再引入假设,傅里叶级数形式为有限个[c0,c1,⋯,cN−1]:
f(kNT)=c0w0k+c1w1k+c2w2k⋯+cN−1w(N−1)k(4.5)
将(4.5)写成矩阵形式,进行解方程组计算。
⎣⎡f(0NT)f(1NT)f(2NT)f(3NT)⋮f((N−1)NT)⎦⎤=⎣⎡1111⋮11ww2w3⋮wN−11w2w4w6⋮w2(N−1)1w3w6w9⋮w3(N−1)⋯⋯⋯⋯⋮⋯1wN−1w2(N−1)w3(N−1)⋮w(N−1)2⎦⎤⎣⎡c0c1c2c3⋮cN−1⎦⎤
注意: 采样值N一定要大于等于f(x)的傅里叶级数的个数,才能实现对系数cn的求解。否则会导致cn的重合
-
序列傅里叶变换
令:x(n) = x(nT);ΩT=ω
X(ejω)=n=−∞∑∞x(n)e−jωn(5.1)
-
离散傅里叶变换
X(k)=n=0∑N−1x(n)WNnkWNnk=e−jN2πnk(5.2)
对于序列傅里叶变换而言: ΩT=ω, T=Fs1为信号的采样周期。对于离散傅里叶变换而言:可以将 ω=N2πk。整理两个方程,就能将离散傅里叶变换的频率变量 k 换算为真实的角频率 Ω。
Ω=Tω=k2πNFs(5.3)
其中:Fs为时域信号的采样频率;N为离散傅里叶变换的点数。
加速离散傅里叶变换计算的算法。
将上述方程组进行改写:
⎣⎡1111⋮11wˉwˉ2wˉ3⋮wˉN−11wˉ2wˉ4wˉ6⋮wˉ2(N−1)1wˉ3wˉ6wˉ9⋮wˉ3(N−1)⋯⋯⋯⋯⋮⋯1wˉN−1wˉ2(N−1)wˉ3(N−1)⋮wˉ(N−1)2⎦⎤⎣⎡f0f1f2f3⋮fN−1⎦⎤=⎣⎡c0c1c2c3⋮cN−1⎦⎤
定义wˉk:
wˉk=e−kN2πi(4.6)
交换顺序,矩阵乘积的结果不变。

1)对于傅里叶的共轭矩阵将偶数列排在前,将奇数列排在后(编号从0开始)。
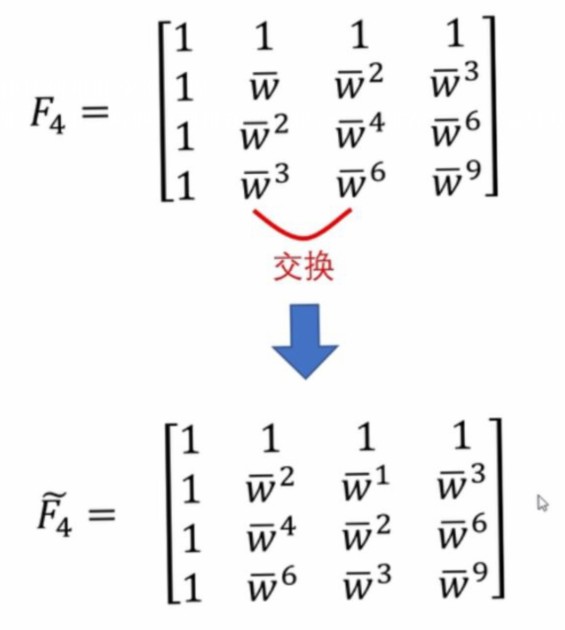
2)对交换后的矩阵进行分块
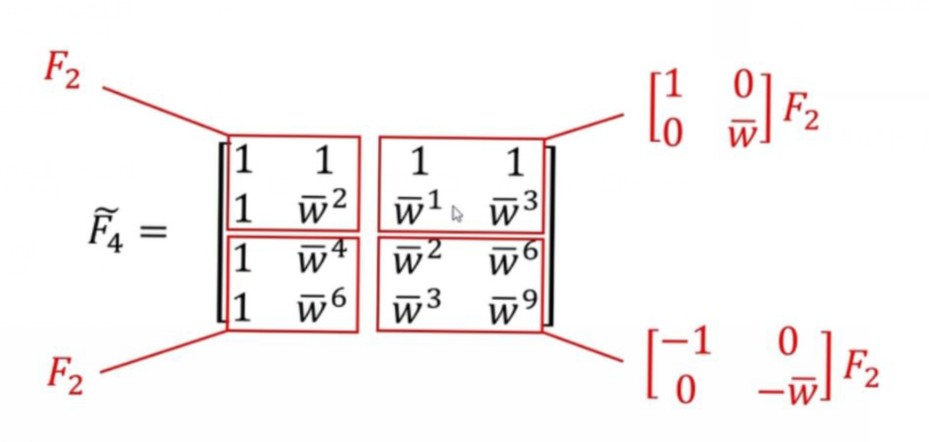
注意:
- 子块F2并不是采样数为2时的傅里叶共轭矩阵;
- wˉk,当N=2n≥4时,对于wˉ2N=−1;(此时采样点在园上对半分,第2N个采样点就刚好在负实轴上。)
- 上述分块法用于N=2n的情况;
3)将分块公式一般化
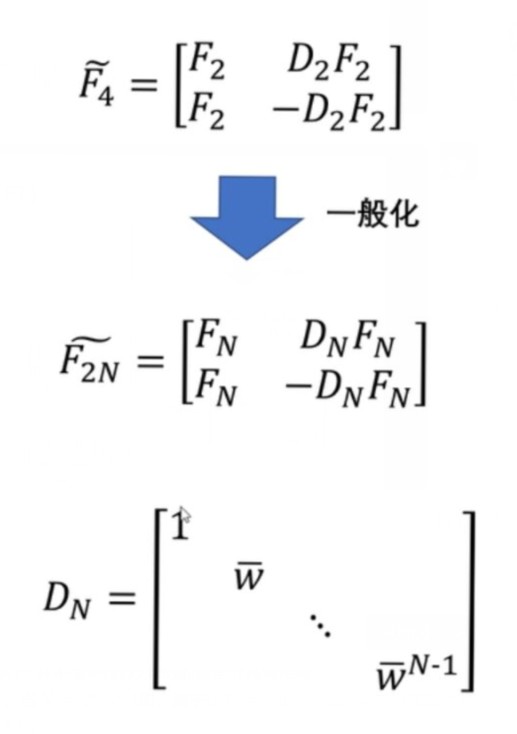
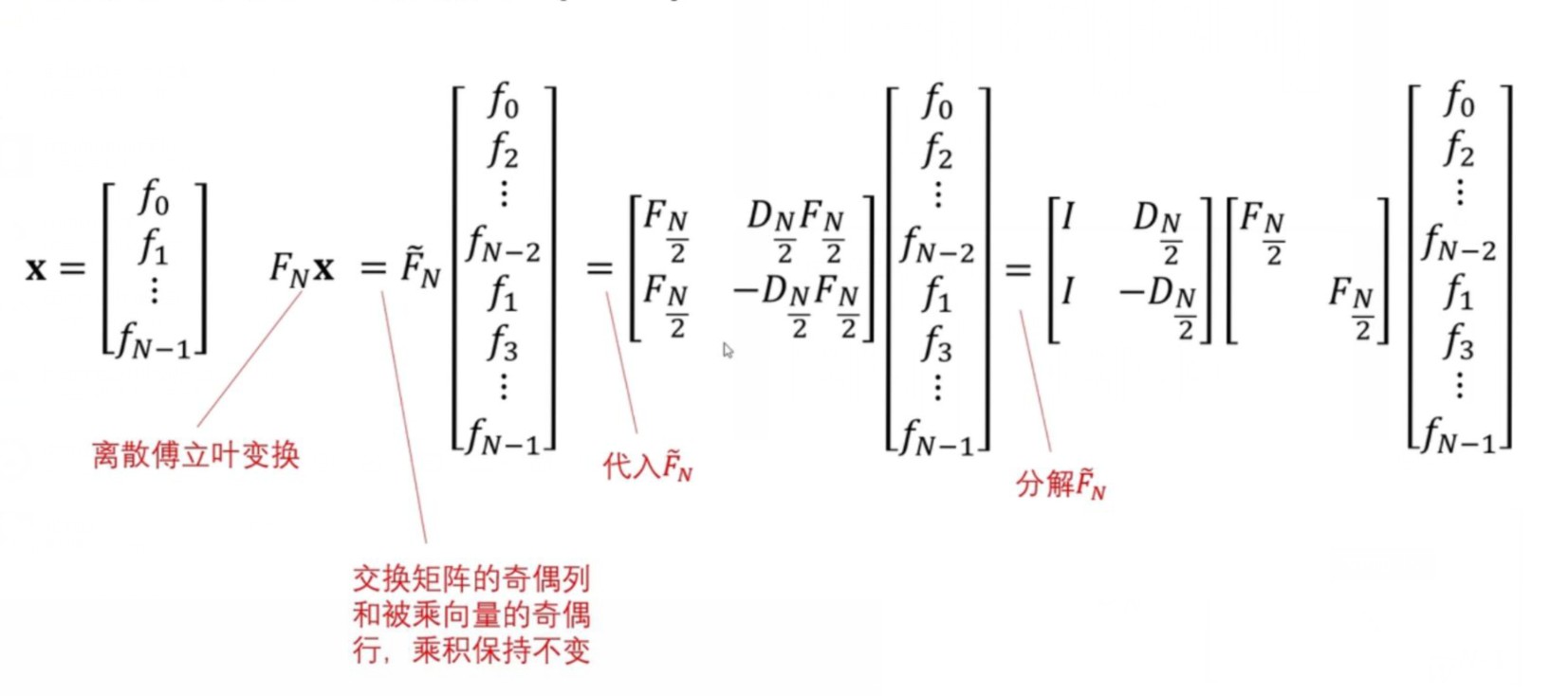
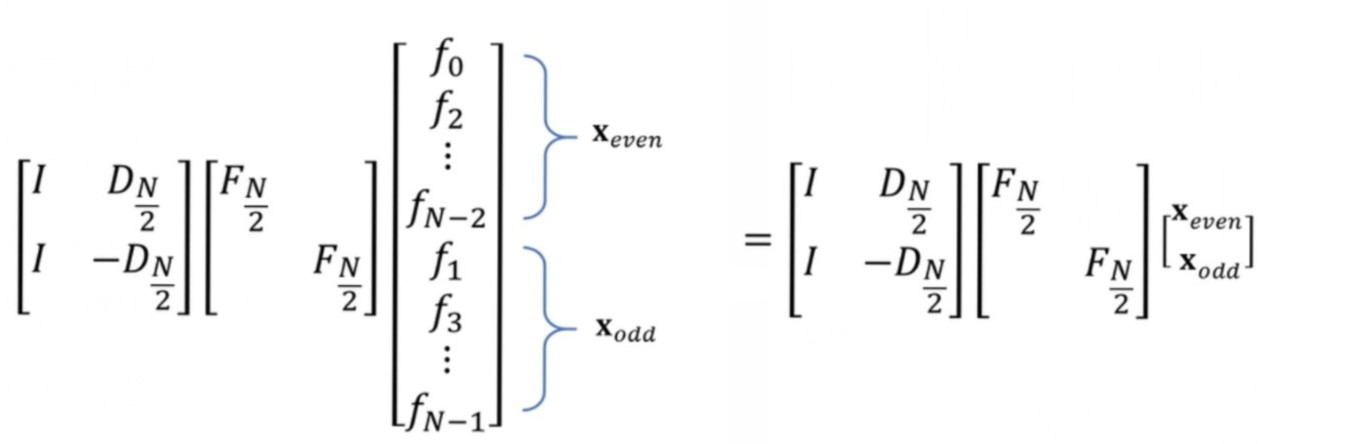
4)获得递推式,实现快速傅里叶算法计算公式l
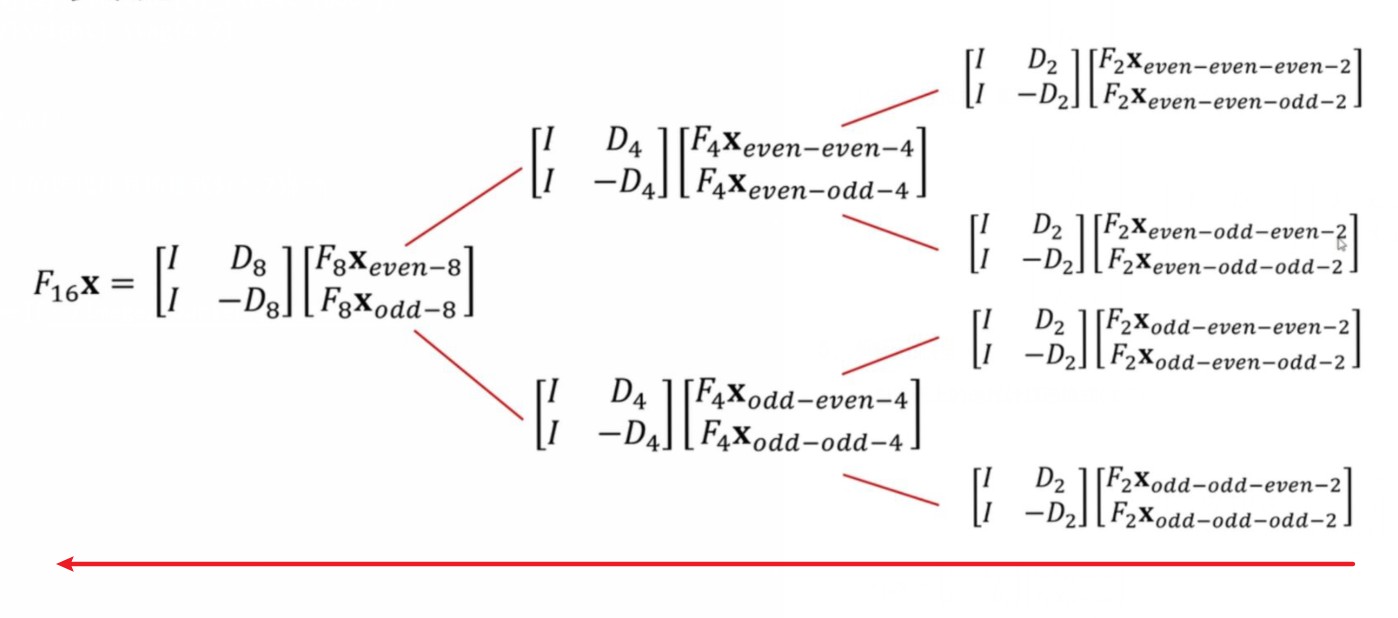
FN⎣⎡f0f1f2f3⋮fN−1⎦⎤=[IID2N−D2N][F2Nxeven F2Nxodd ](4.7)
自下而上的迭代计算递推式(4.7)