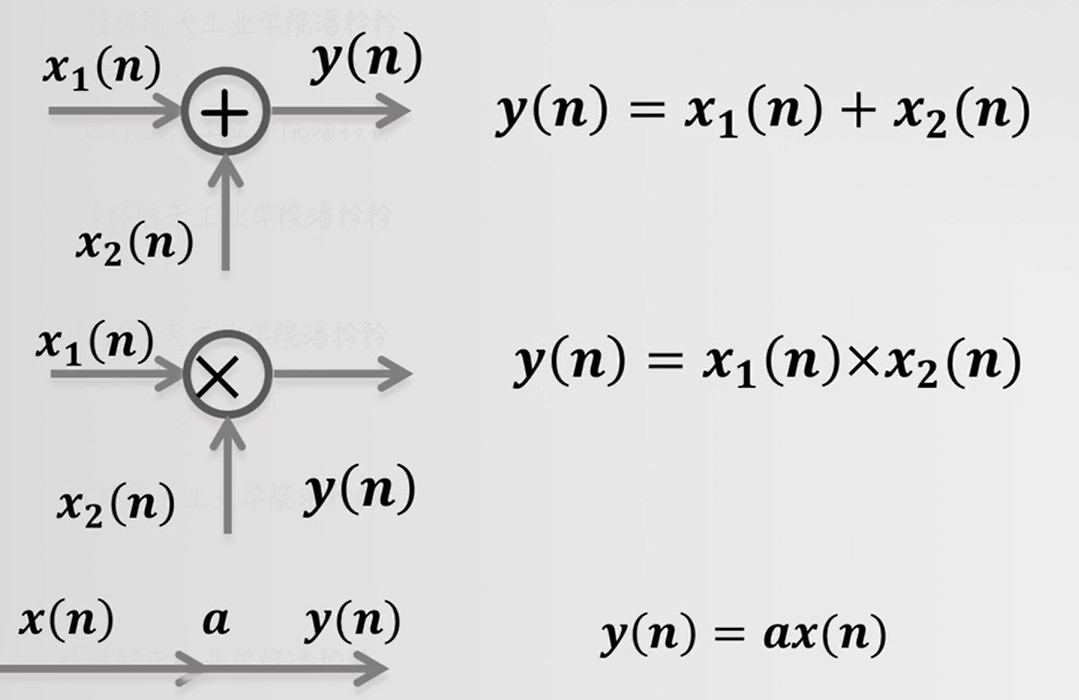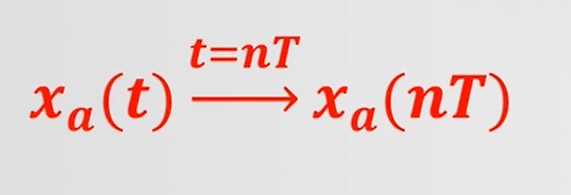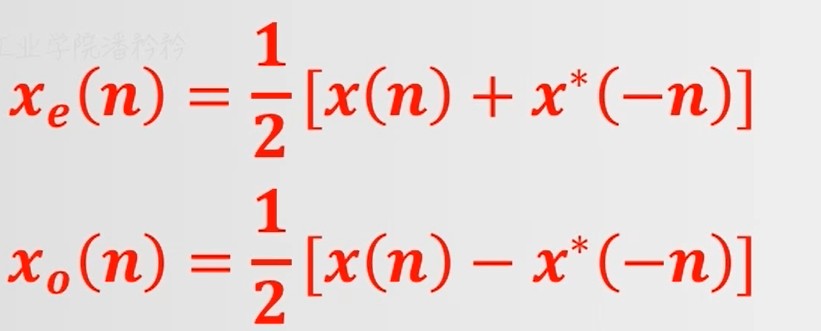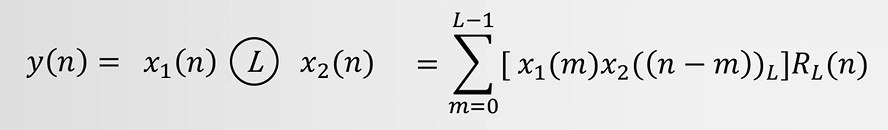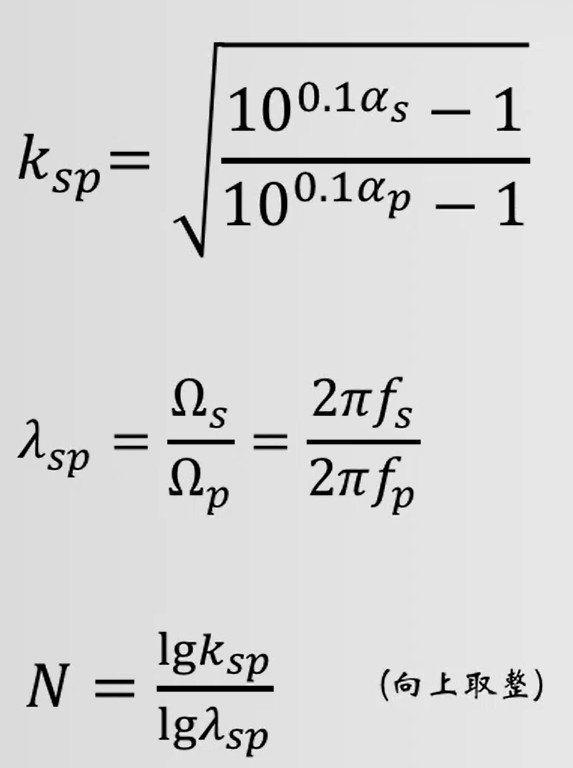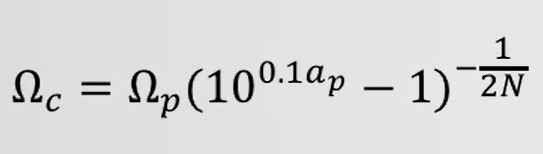数字信号处理
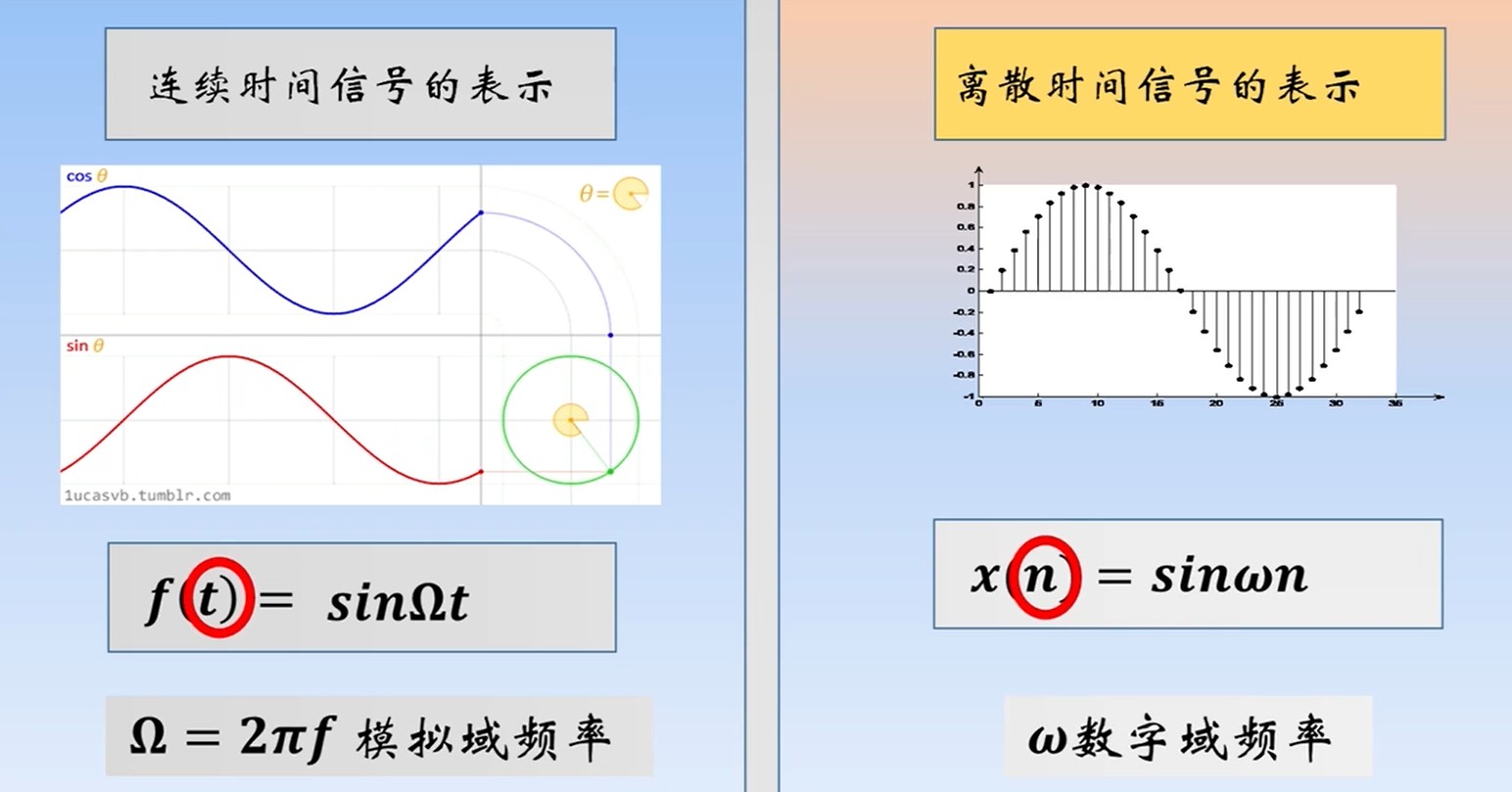
驱动的变量为次数n,而非时间。
-
集合表示
x(n)={1,2,4,6,5,⋯}(1.1)
-
公式
x(n)=sin(ωn), n为样本数
-
图像
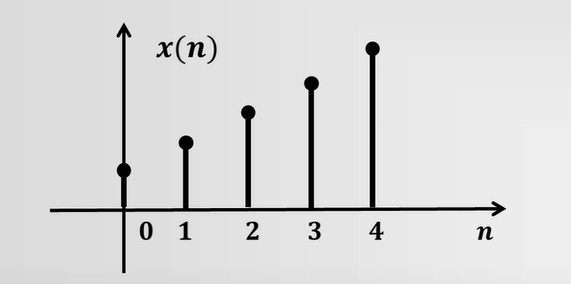
-
单位脉冲序列 δ(n)
δ(n)={⋯,0,1,0,⋯}(1.2)
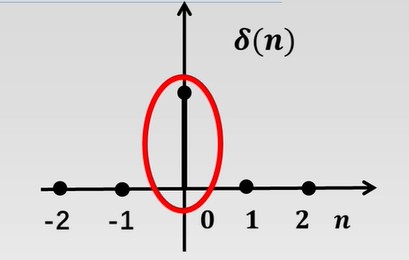
所有的数字信号,都能通过单位脉冲的缩放,偏移,叠加得到。
-
单位阶跃序列 u(n)
u(n)={⋯,0,1,1,1,⋯}(1.3)
-
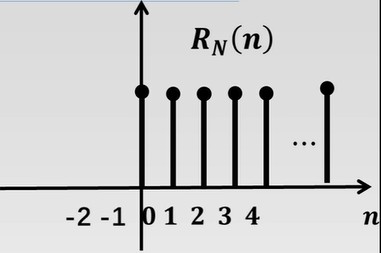
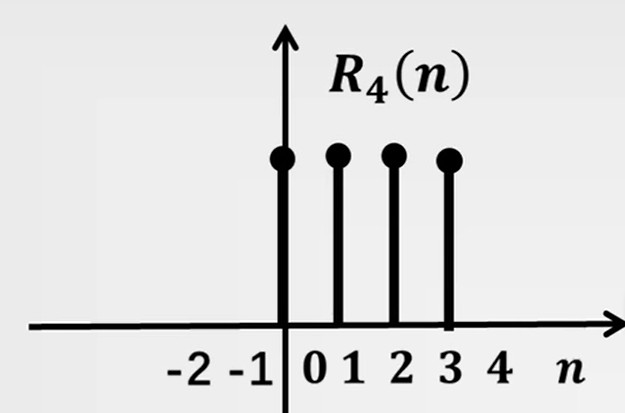
单位矩形序列 RN(n)
RN(n)={⋯,0,1,1,1,⋯,0,0}(1.4)
-
实指数序列 anu(n)
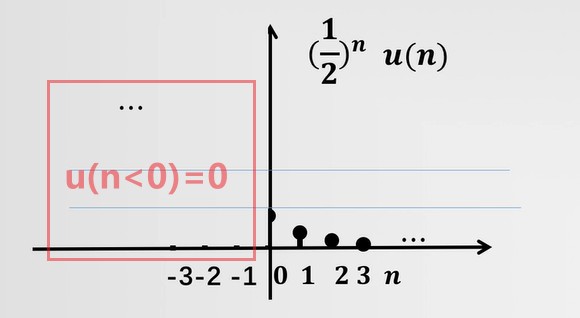
如图,左边全为0,右边有值的序列又称之为:单边序列。
-
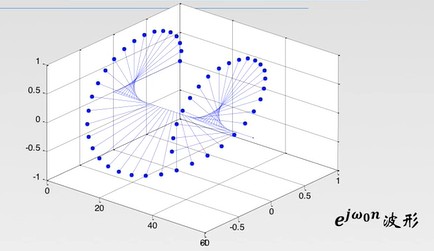
复指数序列 e(σ+jω0)n
e(σ+jω0)n=eδ(cos(ω0n)+jsin(ω0n))(1.5)
-
正弦 sin(ω0n)
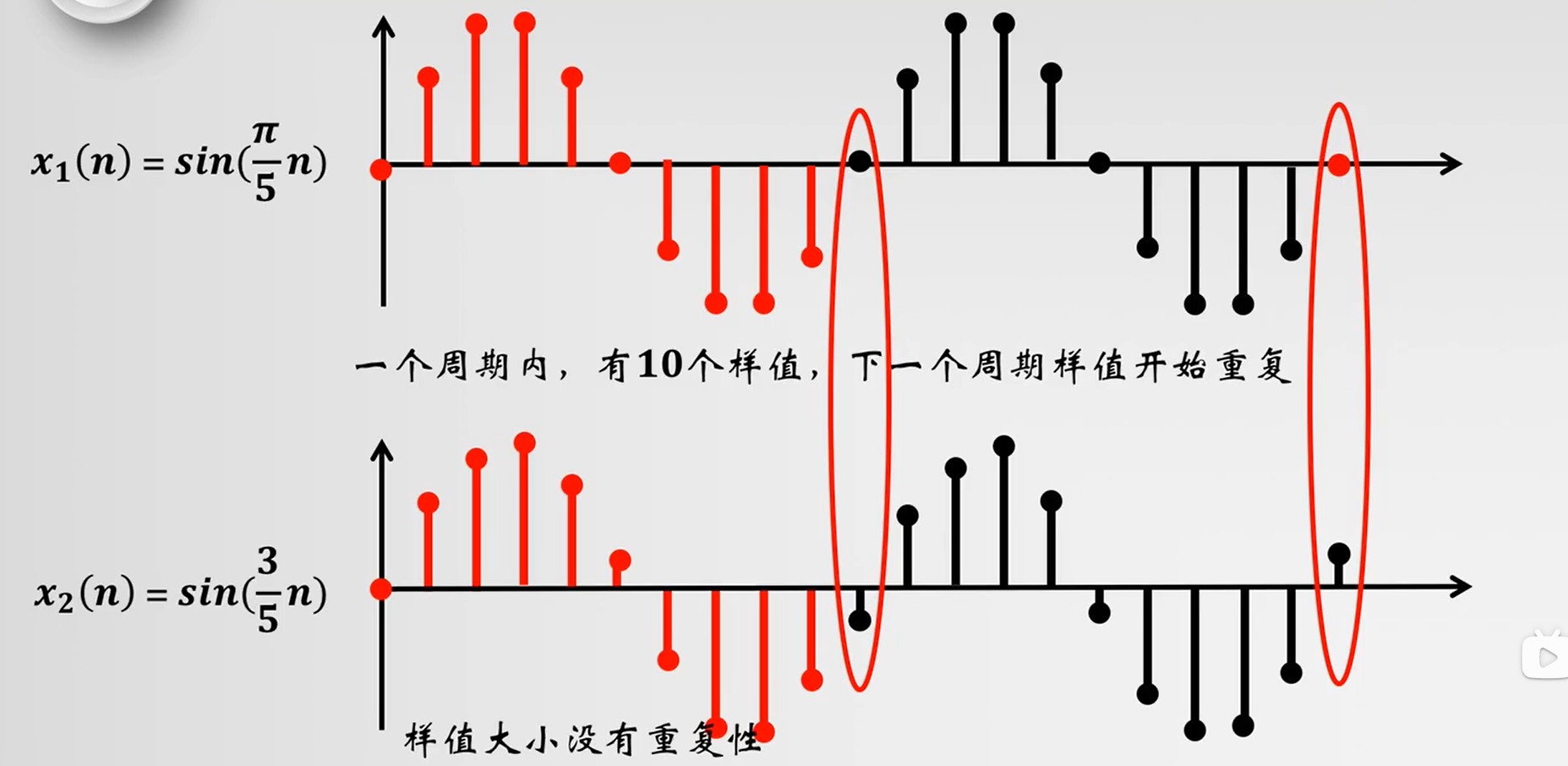
正弦的离散采样值,不一定是周期循环的。
-
周期序列
x(n)=x(n+N);N是整数。(1.6)

当多个正弦叠加时,周期为所有正弦信号的公倍数。
-
加减乘除
n对齐后,直接各个对应采样值进行加减乘除
-
位移,翻转
位移:x(n-N),左加右减
翻转:x(-n)
-
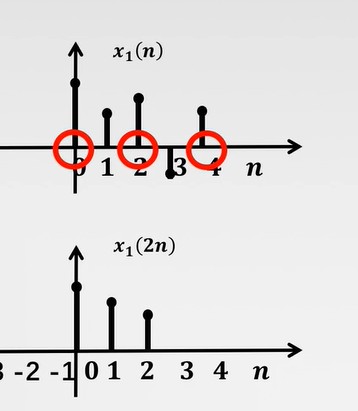
尺度变换
x(an) :序列x(n)每间隔a个点取一个点,构成一个新的序列。
-
加减,乘除,倍增
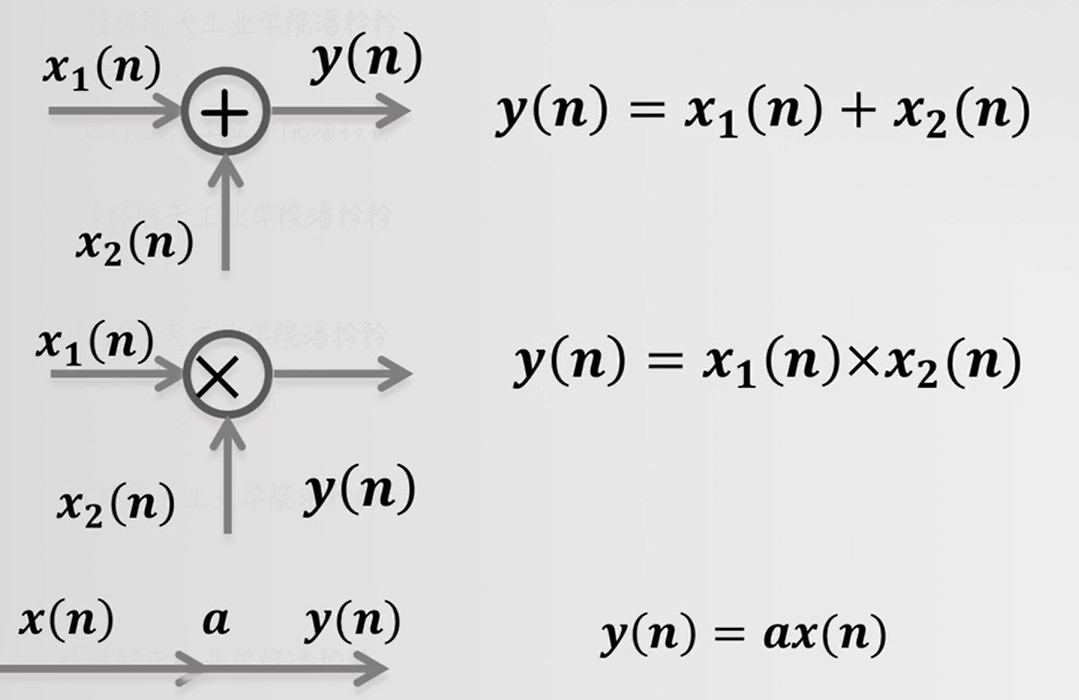
-
函数运算
- 定义:系统的输入输出之间满足线性叠加原理。
- 判断原则: 是用系统进行判定,而不是用单位脉冲响应h(n)进行判定
设:y1(n)y2(n)则:y1(n)+y2(n)=T[a1x1(n)]=T[a2x2(n)]=T[[a1x1(n)+a2x2(n)](2.1)
- 定义:系统对于输入信号的运算关系在整个过程中不随时间变化。
- 判断原则: 是用系统进行判定,而不是用单位脉冲响应h(n)进行判定
设:y(n)则:y(n−n0)=T[ax(n)]=T[ax(n−n0)](2.2)
同时满足上述的2.2和2.3的系统。
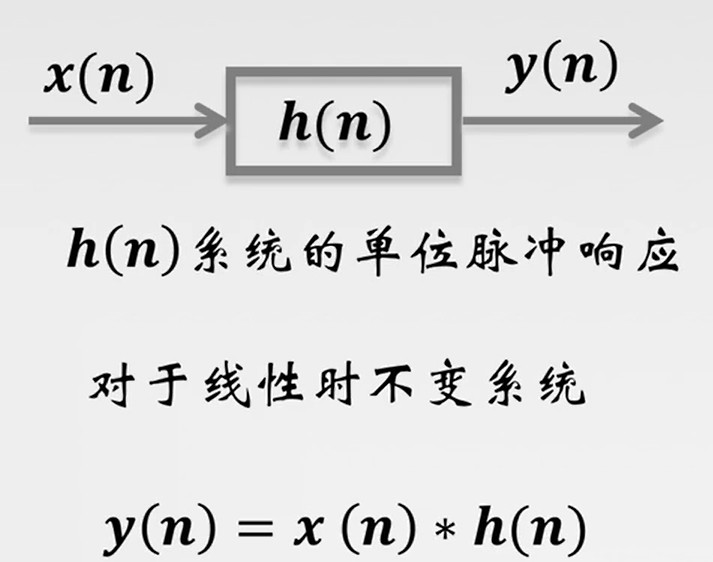
系统输入δ(n)时,系统输出就是单位脉冲响应。
h(n)=T[δ(n)](2.3)
对于 线性时不变系统 系统的输出可以通过 单位脉冲响应和系统输入卷积计算得到。
y(n)=x(n)∗h(n)=k∑x(k)h(n−k)(2.4)
- 交换律:a * b = b * a
- 结合律:(a * b) * c = a * (b * c)
- 分配律:a * (b + c) = a*b + a * c
-
因果性
定义: 系统的输出不发生在输入之前。超前系统没有因果性。 通过系统进行判定
y(n)y(n)y(n)=ax(n)+b=ax(n−1)+b;滞后=ax(n+1)+b;超前(2.5)
线性时不变系统的判定: 充要条件为,当 n<0 时,h(n)=0;即 系统的初始储能为0。 通过单位脉冲响应判定h(n)
-
稳定性
定义: 对有界限的输入,系统产生的输出也是有界的。 通过系统进行判定
线性时不变系统的判定: 系统的单位脉冲响应 绝对可和;∑n=−∞∞∣h(n)∣<∞。 通过单位脉冲响应判定h(n)
-
D延时

y(n)y(n)=1,2,3,⋯=0,1,2,3,⋯(3.1)
-
常系数差分方程
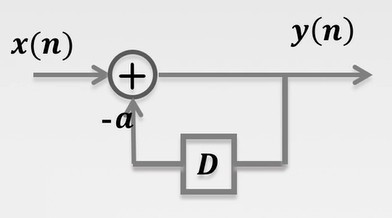

y(n)+ay(n−1)y(n)+ay(n−1)+by(n−2)⋯=x(n);一阶常系数差分方程=x(n);二阶常系数差分方程(3.2)
定义: 有几个D延时,就是几阶。
定义:求解差分方程,就是计算y(n)值。
- 经典法:直接算y(n)的公式
- 递推法: 根据 初始条件 和 递推式 进行递推求解y(n)
- z变换法
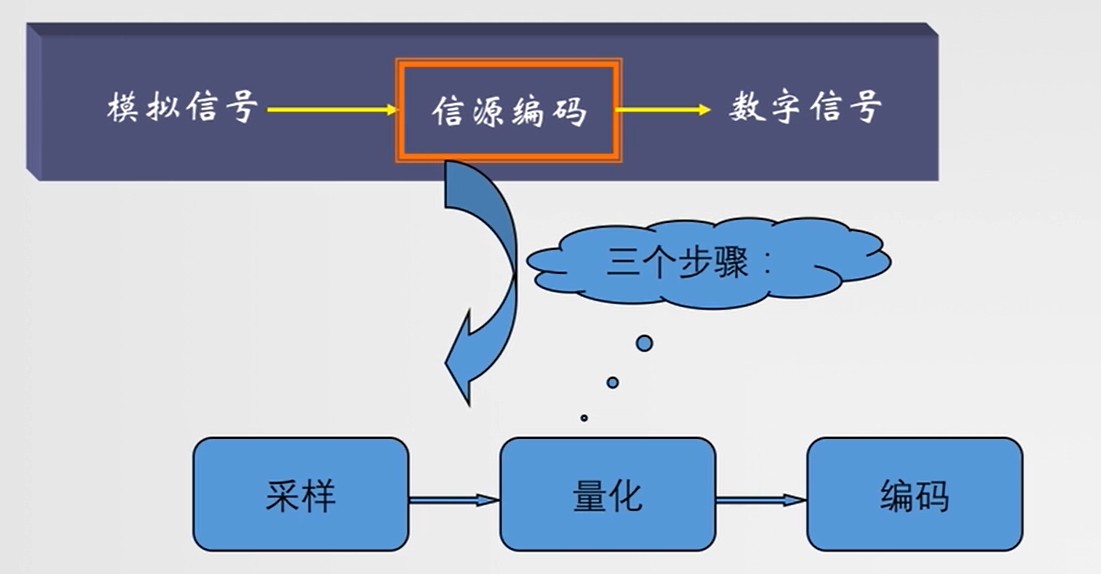
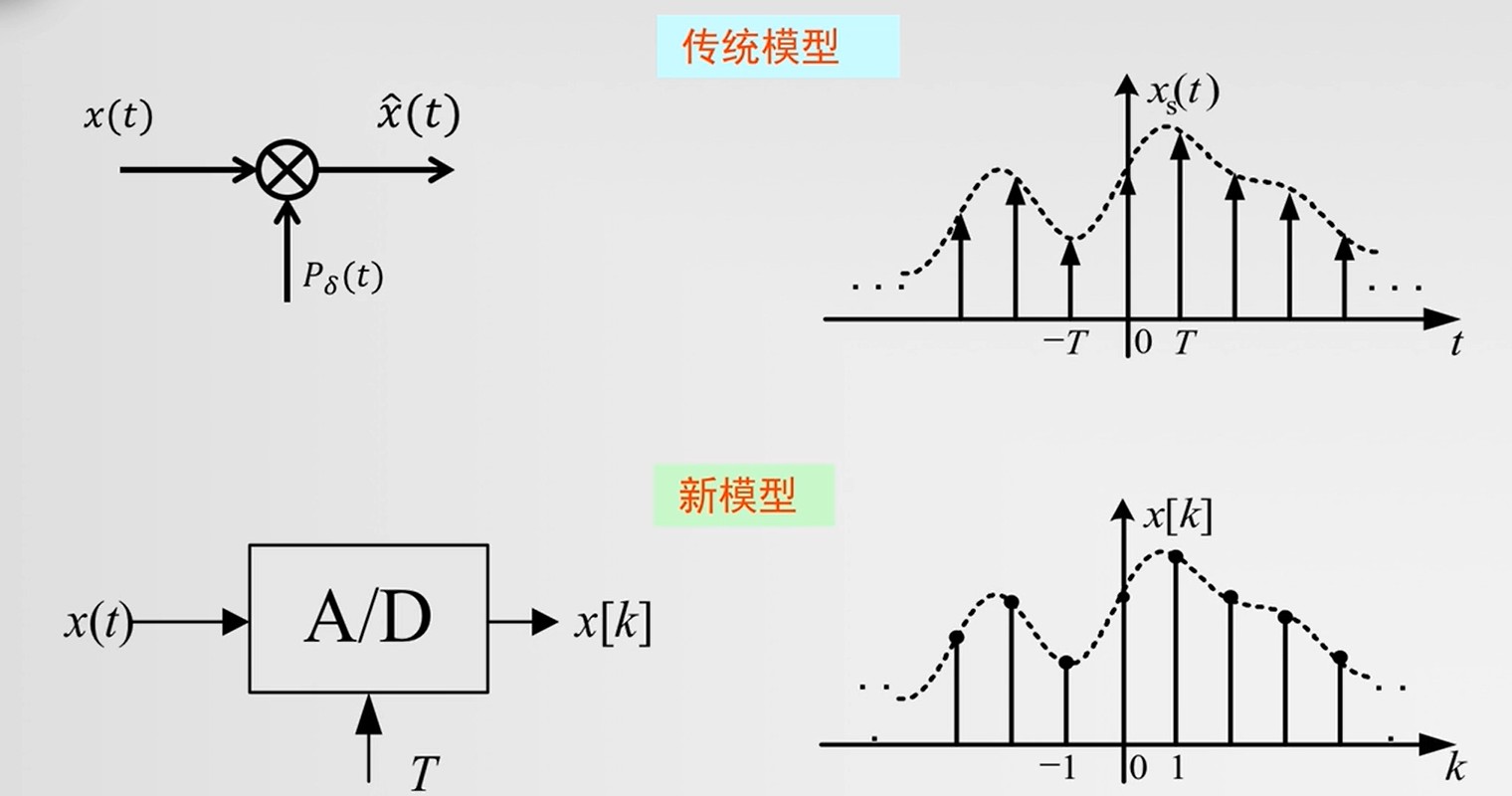
- 传统模型:只完成了采样
- A/D转换器:直接完成三个步骤,输出数字信号

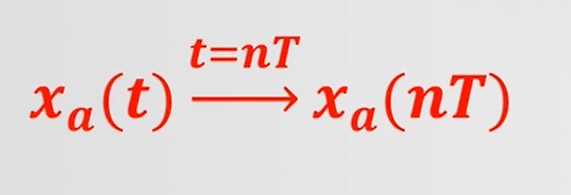
源信号频谱:
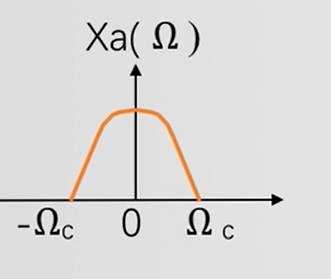
采样信号的频谱:
奈奎斯特采样定律:采样频率 Ωs≥2Ωc,就能唯一恢复源信号。
注意:
- 角频率与频率不一样
- 频率是 T1,表示的是一秒重复多少次。
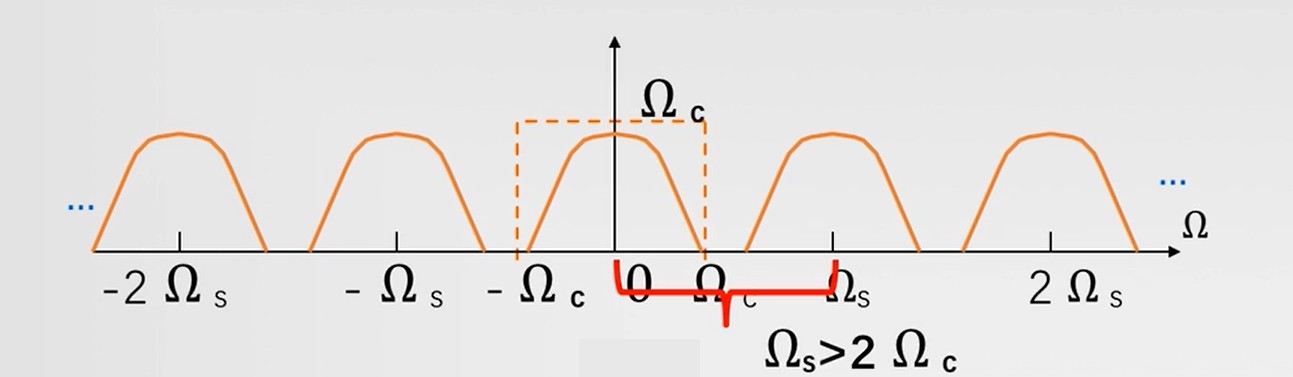
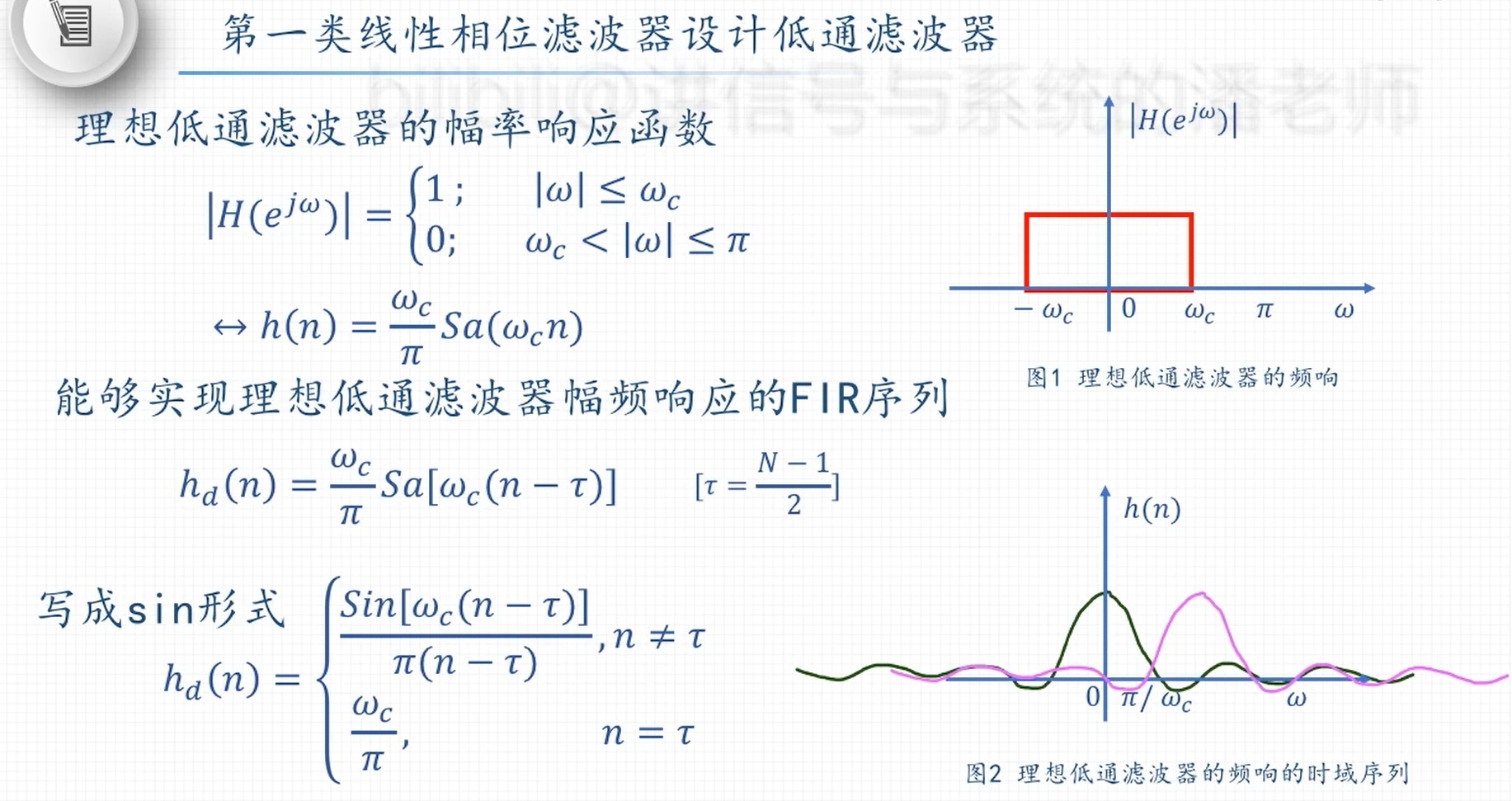
抽样信号的恢复:通过低通滤波器进行恢复。
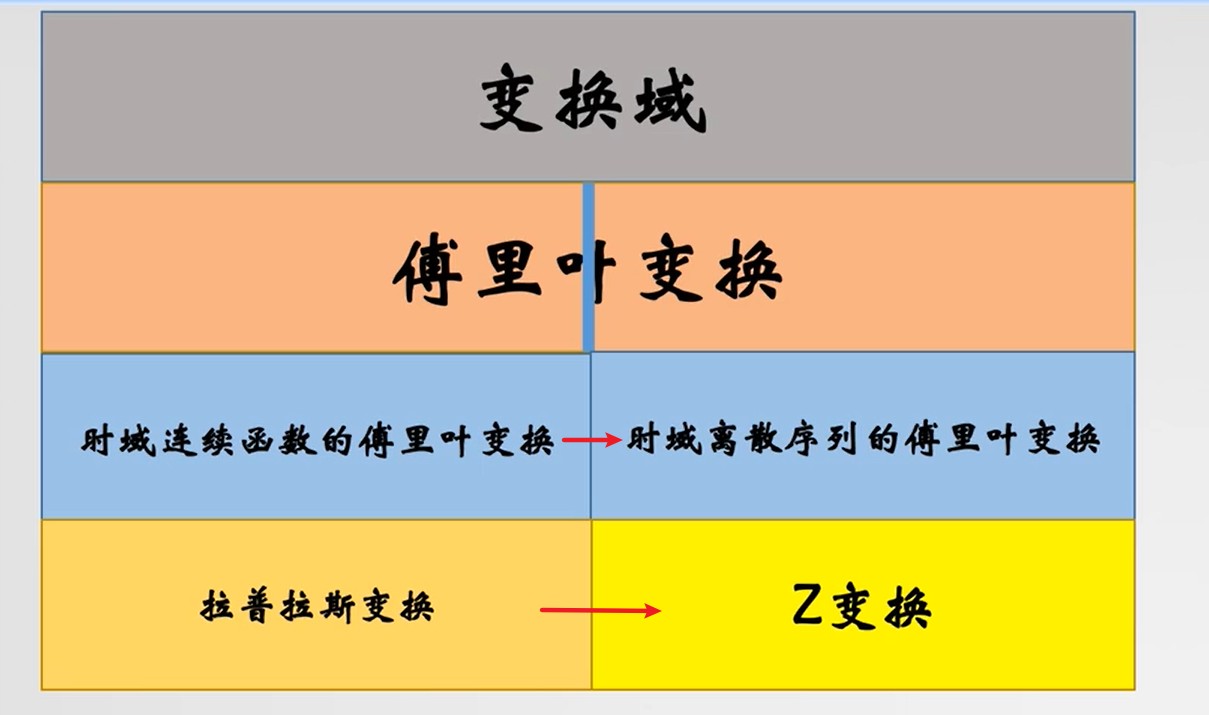
- 采样信号:
x^(t)=n=−∞∑∞x(nT)δ(t−nT)(1.1)
其中:T为采样周期
X(jΩ)=∫−∞+∞x(t)e−jΩtdt=∫−∞+∞[n=−∞∑∞x(nT)δ(t−nT)]e−jΩtdt=n=−∞∑∞x(nT)e−jΩnT(1.2)
-
序列傅里叶变换
令:x(n) = x(nT);ΩT=ω
X(ejω)=n=−∞∑∞x(n)e−jωn(1.3)
存在条件:∑n=−∞∞∣x(n)∣<∞
X(ejω)=1(1.4)
X(ejω)=1−ae−jω1(1.5)
X(ejω)=X(ej(ω+2πM))(1.6)
设:FT[x1(n)]=X1(ejω),FT[x2(n)]=X2(ejω)则:FT[x1(n)+x2(n)]=X1(ejω)+X2(ejω)(1.7)
时移:FT[x(n−n0)]=e−jωn0X(ejω)频移:FT[ejω0nx(n)=X(ej(ω−ω0)](1.8)
设:y(n)=x(n)∗h(n)则:Y(ejω)=X(ejω)H(ejω)(1.9)
设:y(n)=x(n)h(n)则:Y(ejω)=2π1X(ejω)∗H(ejω)(1.10)
n=−∞∑∞∣x(n)∣2=2π1∫−ππ∣X(ejω)∣2(1.11)
设:z=x+yjz=rejω共轭复数:z∗=x−yjz∗=re−jω(1.12)
- x(−n),x∗(n),x∗(−n)
FT[x(−n)]FT[x∗(n)]FT[x∗(−n)]=X(e−jω)=X∗(e−jω)=X∗(ejω)(1.13)
-
共轭对称与反对称序列
共轭对称序列: x(n)=x∗(−n);虚部为0,为 偶序列
共轭反对称序列: x(n)=−x∗(−n);虚部为0,为 奇序列
-
共轭对称与反对称函数
共轭对称函数: X(ejω)=X∗(e−jω)
共轭反对称函数: X(ejω)=−X∗(e−jω)
由于序列傅里叶变换与连续傅里叶变换同样存在这成立条件,采用拉普拉斯的思路方案,可以将序列傅里叶变换的使用范围拓宽,这个就是Z变换。 z变换存在收敛域,就是a能不能存在。
定义一个数 a−n,可以驱使x(n)满足序列傅里叶变换的存在条件:
X(aejω)=n=−∞∑∞x(n)a−ne−jωn(2.1)
令:z=aejω
X(z)=n=−∞∑∞x(n)z−n(2.2)
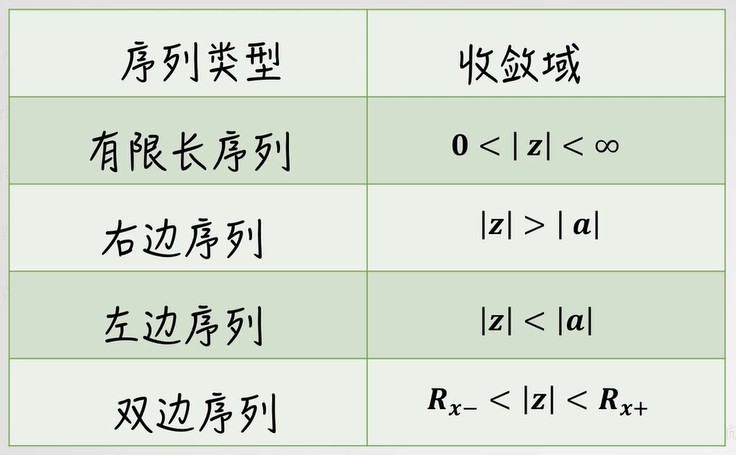
因果序列是右边序列的一种;因果序列是物理上能实现的。
设Z[x(n)] = X(z),则 y(n)=anx(n)的z变换为:Y(z)=X(a−1z)。
Z[nx(n)]=−zdzdX(z)(2.7)
x(0)=z→∞limX(z)(2.8)
x(∞)=z→1lim(1−z)X(z)(2.9)

-
定义: 已知序列的z变换X(z),求原序列x(n)变换称为 z反变换。
-
通式: 所有的z变换公式都能化解为有理分式形式。
X(z)=D(z)N(z)=anzn+an−1zn−1+⋯a1z+a0bmzm+bm−1zm−1+⋯b1z+b0(3.1)
- 极点pk: D(z)=0
- 零点zk: N(z)=0
主要引用了:实指数的z变换;z变换的线性。

-
差分方程
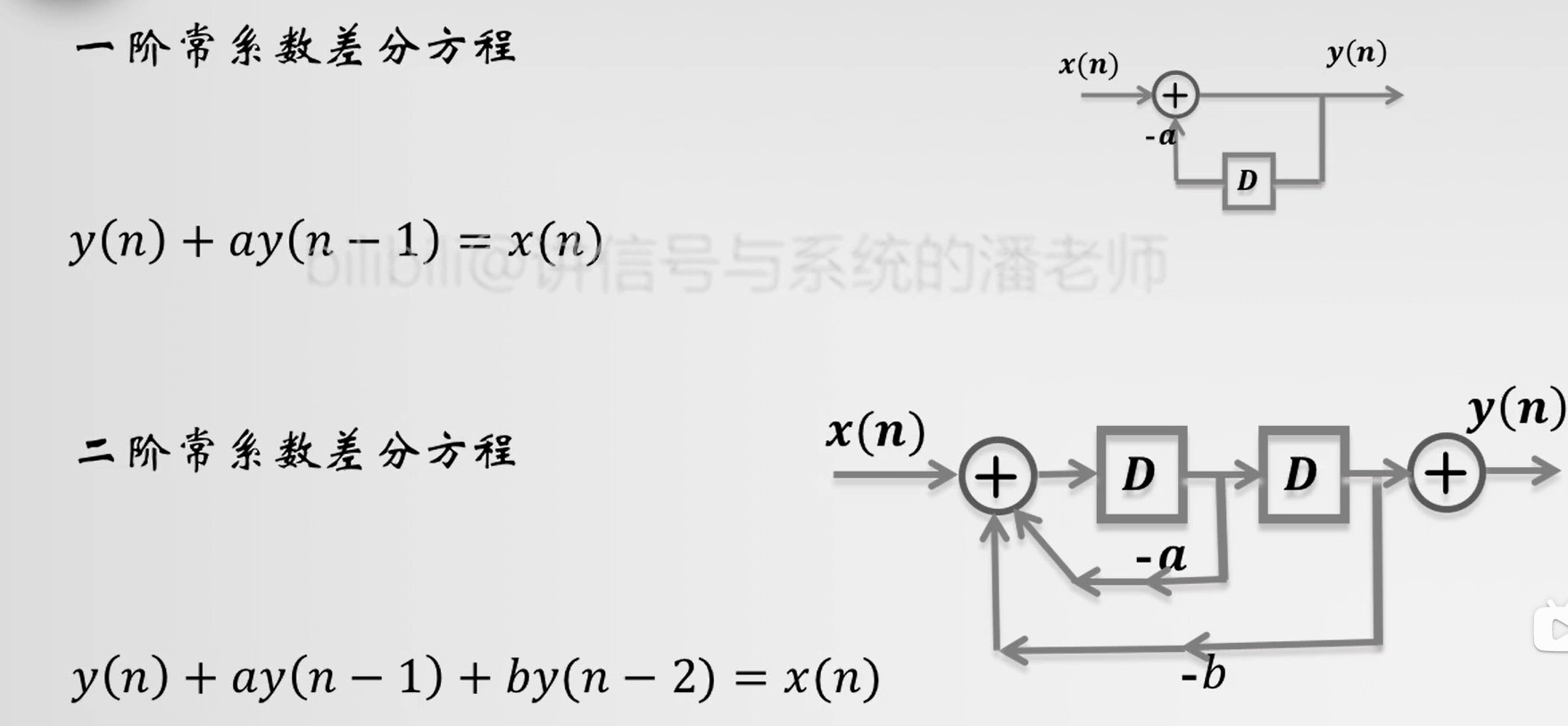
-
z的位移变换

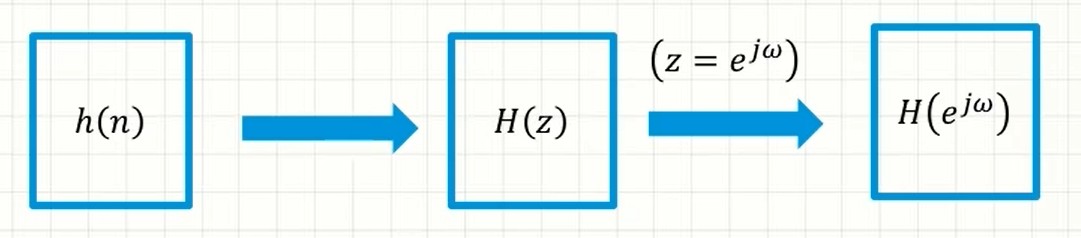
H(ejω)=∣H(ejω)∣ejϕ(ω)(5.2)
幅频特性:∣H(ejω)∣
相频特性:ϕ(ω)
y(n)=h(n)∗x(n)=m=−∞∑∞h(m)x(n−m)=m=−∞∑∞h(m)ejω0(n−m)=ejω0nm=−∞∑∞h(m)e−jω0m=ejω0nH(ejω0)=∣H(ejω0)∣ej(ϕ(ω0)+nω0)(5.3)
-
频响的距离
求:∣1−z∣设:z=a+jb则:∣1−z∣2=∣(1−a)−jb∣2=(1−a)2+b2(5.4)
对于(1 - z)而言,(1,0)就是一个零极点。对于圆 (1−a)2+b2=R2 而言,(1,0)又是一个圆心,且 模 R=|1 - z| 为半径。
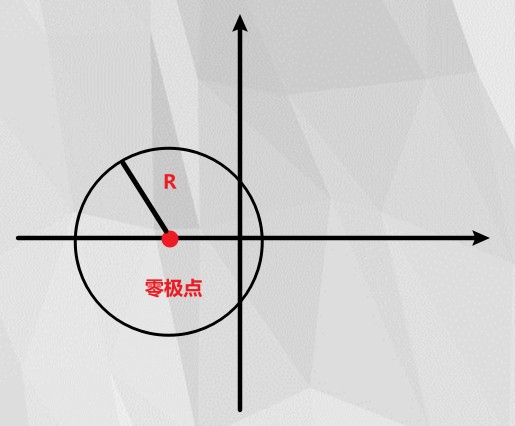
由于 H(z) 频响中的 z=ejω ,因此,z的变化应该是在一个单位圆上。
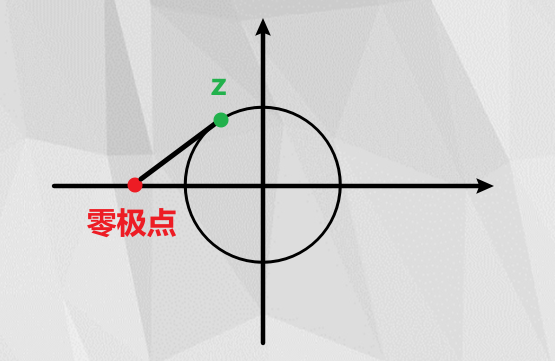
-
幅频响应特性
H(z)=(1−a1z−1)(1−a2z−1)⋯(1−b1z−1)(1−b2z−1)⋯(5.5)
∣H(ejω)∣=所有极点到单位圆上动点的长度之积所有零点到单位圆上动点的长度之积(5.6)
极点:决定曲线峰值
零点:决定曲线谷值
-
相频响应特性
ϕ(ω)=所有极点到单位圆上动点的辐角之和所有零点到单位圆上动点的辐角之和(5.7)
H(z)=X(z)Y(z)(6.1)
n=−∞∑∞∣h(n)∣<∞(6.3)
结论: H(z)收敛域包含单位圆。
用于计算机进行运算。
X(k)=n=0∑N−1x(n)WNnk(2.1)
其中:N,DFT的变换区间长度;k,频率的编号。
WNnk=e−jN2πnk(2.2)
根据序列傅里叶变换可知,离散傅里叶也是周期的,其结果就是在对序列傅里叶变换的结果进行抽样。
根据傅里叶存在定理,周期序列不满足绝对可和条件,因此周期序列就不存频谱。 对于这个问题需要利用傅里叶级数来解决。
周期序列的傅里叶级数:
x~(k)=n=0∑N−1x~(n)WNnk(3.1)
计算结果为傅里叶级数的系数。 N,为一个周期长度。
| 变换类型 |
特点 |
周期 |
| 连续傅里叶级数 |
时域连续,频域离散 |
时域 |
| 序列傅里叶 |
时域离散,频域连续 |
频域 |
| 离散傅里叶级数 |
时域离散,频域离散 |
频域
时域 |
| 离散傅里叶 |
时域离散,频域离散 |
\ |
结论:要想对频域进行离散采样,时域必须:1)周期;2)离散
将求解离散傅里叶问题,转换为求解离散傅里叶级数问题。
-
表示符号
|
时域 |
频域 |
| 序列 |
x(n) |
X(n) |
| 周期 |
x~(n) |
X~(n) |
-
周期延拓
定义: 将有限长的序列进行重复拼接,就能构造出一个新的周期性序列。
x~(n)=x((n))N=x(n%N)(5.1)
- x~(n) 为 x(n) 的周期延拓序列
- x(n) 为 x~(n) 的主值序列
- ((n))N 表示为求余数:n % N
-
主值序列
X(n)=X~(n)RN(n)(5.2)
注意: 序列从 0 到 N-1 ;4.2式也是原序列x(n)的频谱X(n)计算公式。
-
三种主值序列的构造方式
序列x(n)的长度:M
周期延拓序列的周期(也是DFT的点数):N
- M = N,直接重复序列实现延拓;
- M < N,缺少的用0进行补全;
- M > N,先将序列以N进行拓展,重合部分,进行叠加。(不推荐)
DFT(ax1(n)+bx2(n))N=aX1(k)+bX2(k)(6.1)
其中:x1(n),x2(n)为有限长序列;N >= max(N1,N2)
y(n)=x((n+m))NRN(n)(6.2)
将 x(n) 进行周期延拓,得到 x~(n) ;然后将 x~(n) 向右移动 m 位,得到 x~(n+m)=x((n+m))N;最后取出主值序列 y(n) 。其结果就是有限序列x(n)被循环重排列了。
Y(k)=DFT[y(n)]N=WN−mkX(k)(6.3)
IDFT[X~(k+l)NRN(k)]=WNnlx(n)(6.4)

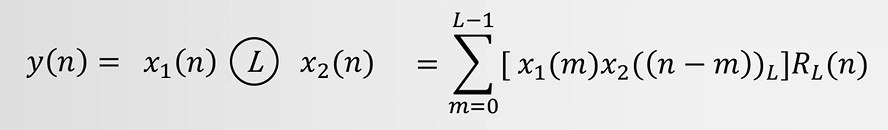
DFT[x∗(n)]NX(N)=X∗(N−k);0≤k≤N−1=X(0);k=N(6.5)

由于DFT变换后,X(k)满足共轭对称性,所以X(k)序列的模是对称分布的,计算结果就只用存一半就行。
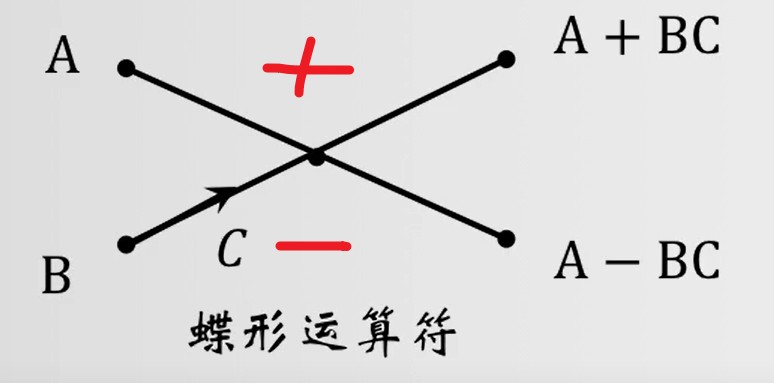
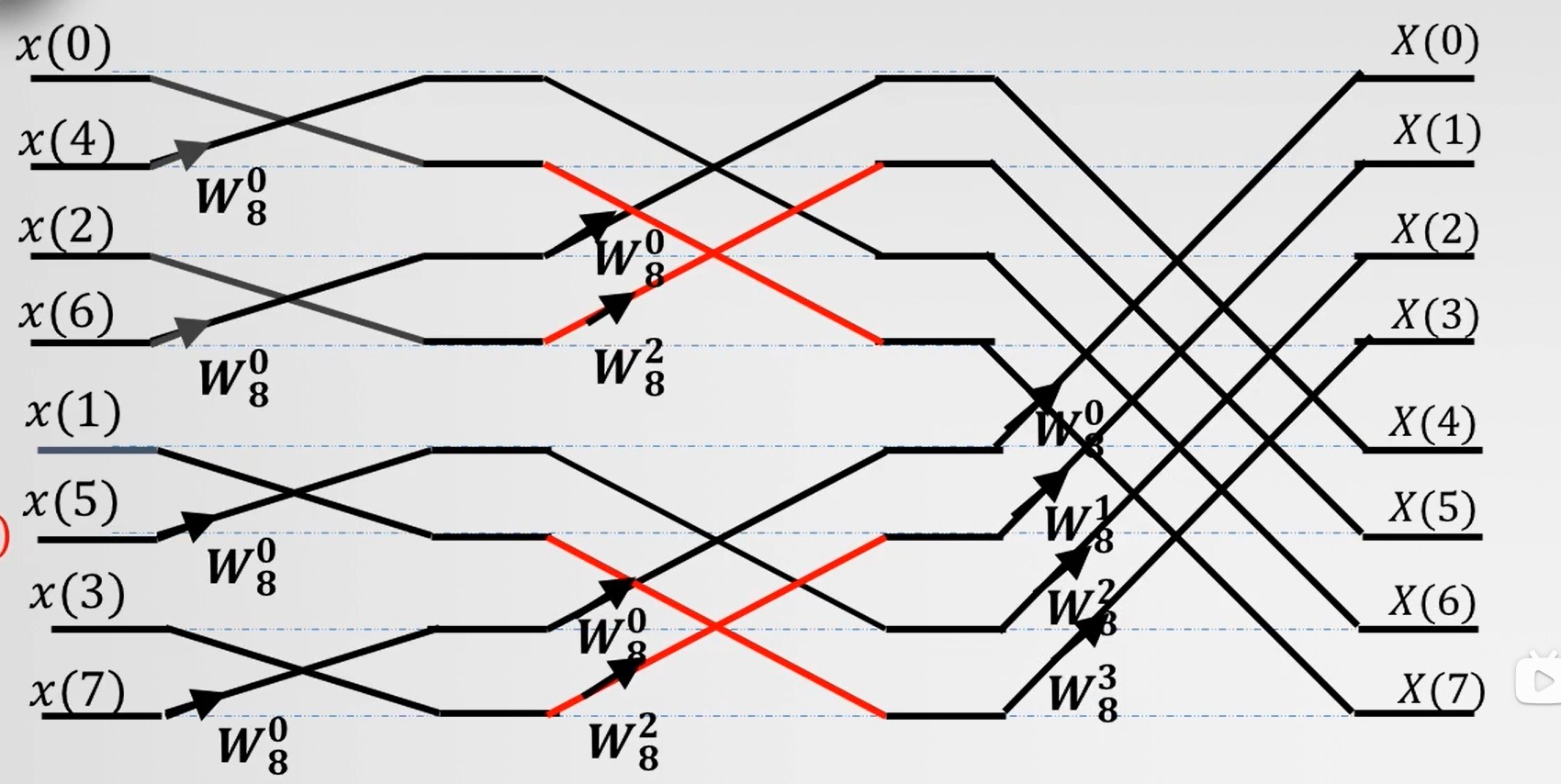
对于N点的DFT:
- 二进制编号的位数:M=log2(N)
- 初始二进制全为0
- 二进制编号就是右边蝶形时域序列的输入点的编号
- 二进制编号加一,向着次高位进位,一直重置
- N点DFT的级数:M=log2(N)
- L级数的旋转因子:WNJ2M−L,J=0,1,2⋯,(2L−1−1)

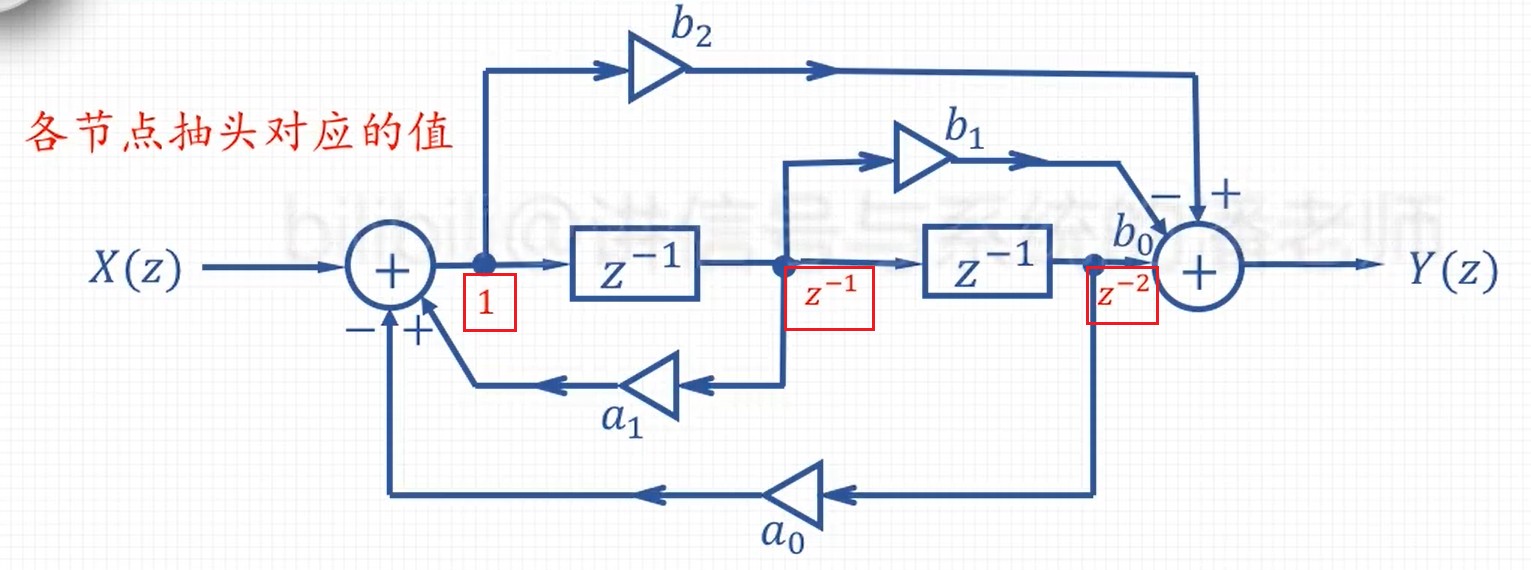
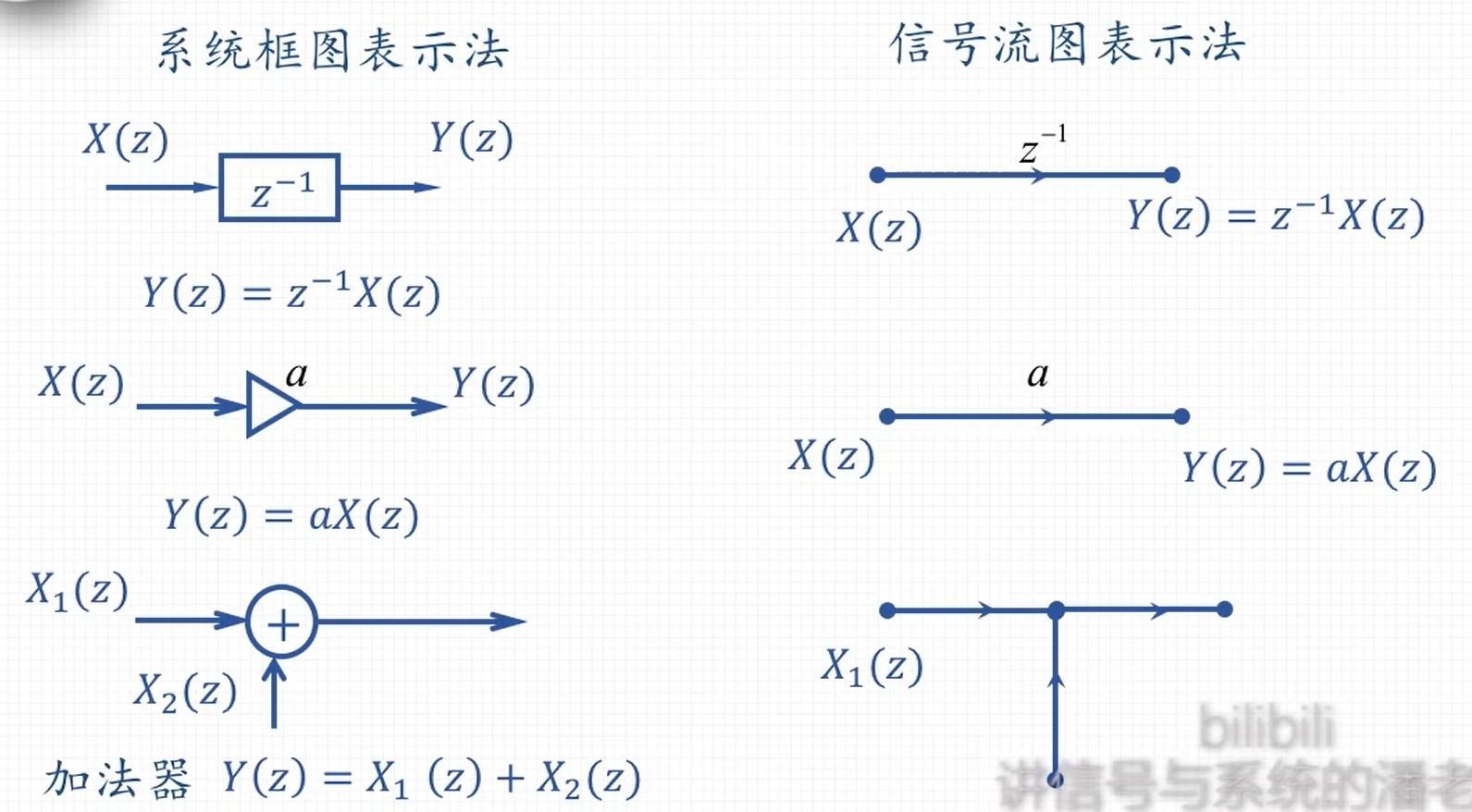
- 第一个节点假设为1,依次计算出主线的各个节点值
- 正向线路:计算 Y(z)=b0z−2−b1z−1+b2
- 反向线路:计算 1=X(z)+a1z−1−a0z−2
- 系统函数:H(z)=1−a1z−1+a0z−2b0z−2−b1z−1+b2
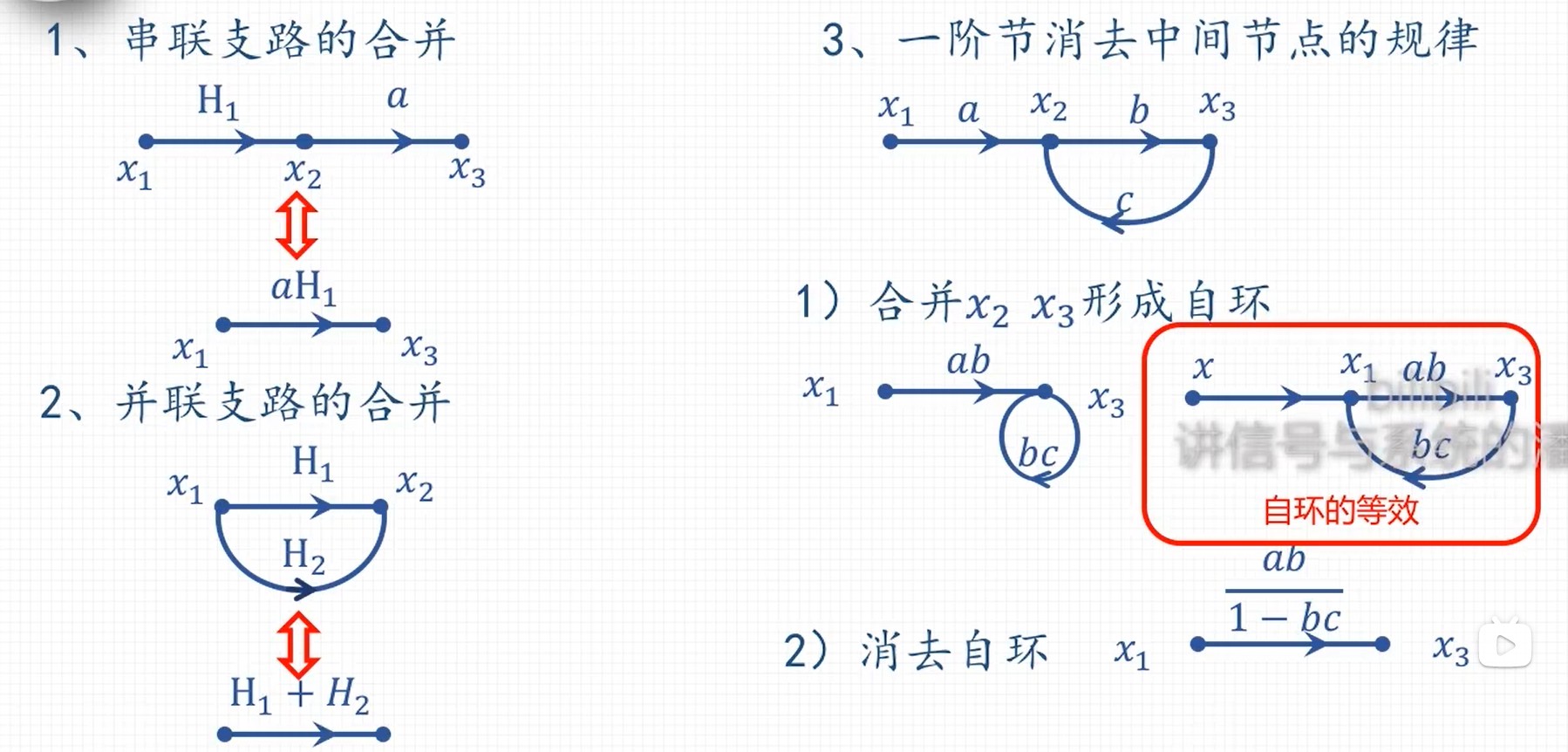
- 线频率: f,每秒时间内信号变化的周期数。
- 角频率: Ω=2πf,每秒时间内信息变化的弧长。
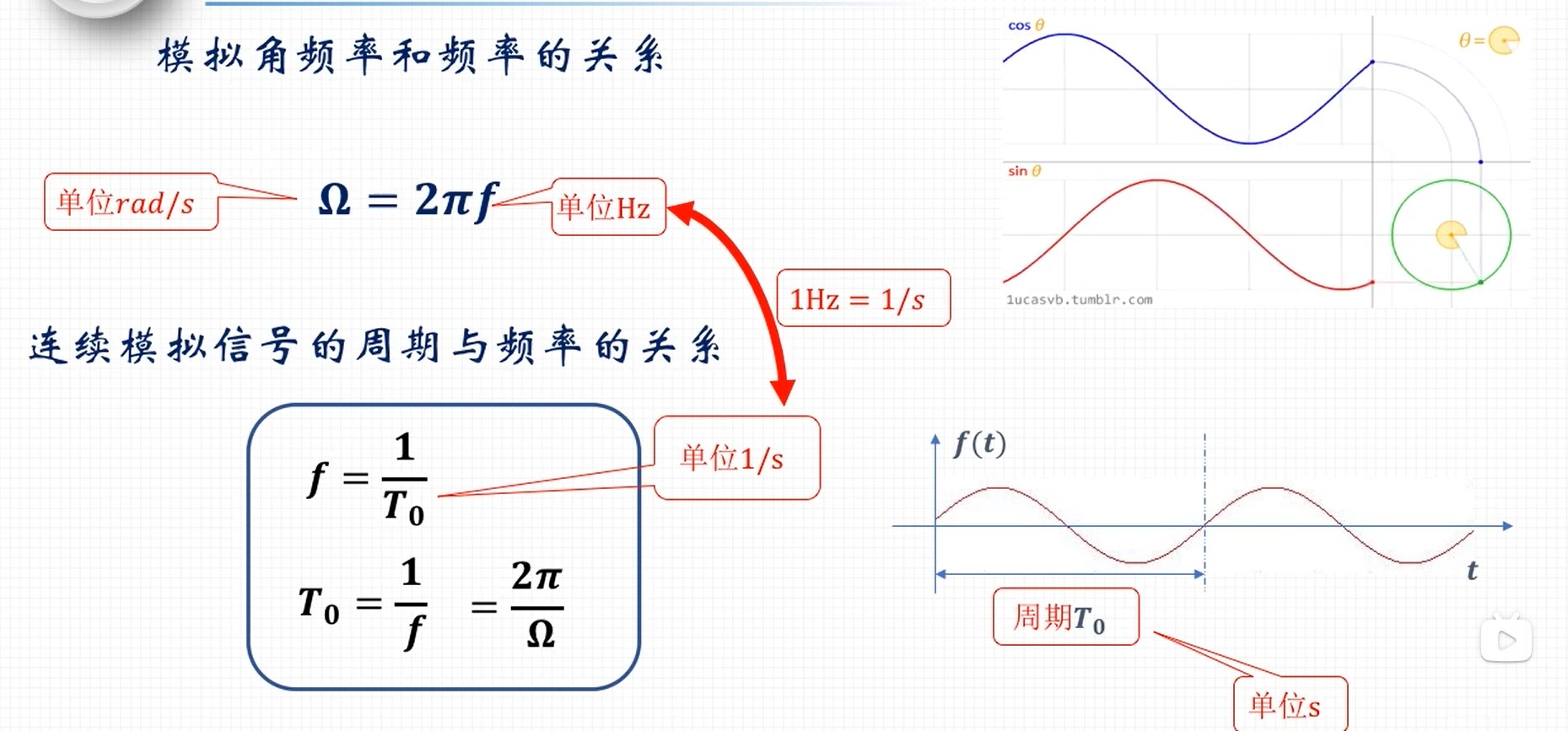
- 采样频率: fs,单位时间内采样的次数
- 数字频率: ω=2πfsf,相邻两个采样点之间变化的弧度。

根据奈奎斯特采样定理:fs≥2f, ω≤π ;数字信号频率:π 就对应着模拟信号的最高角频率。
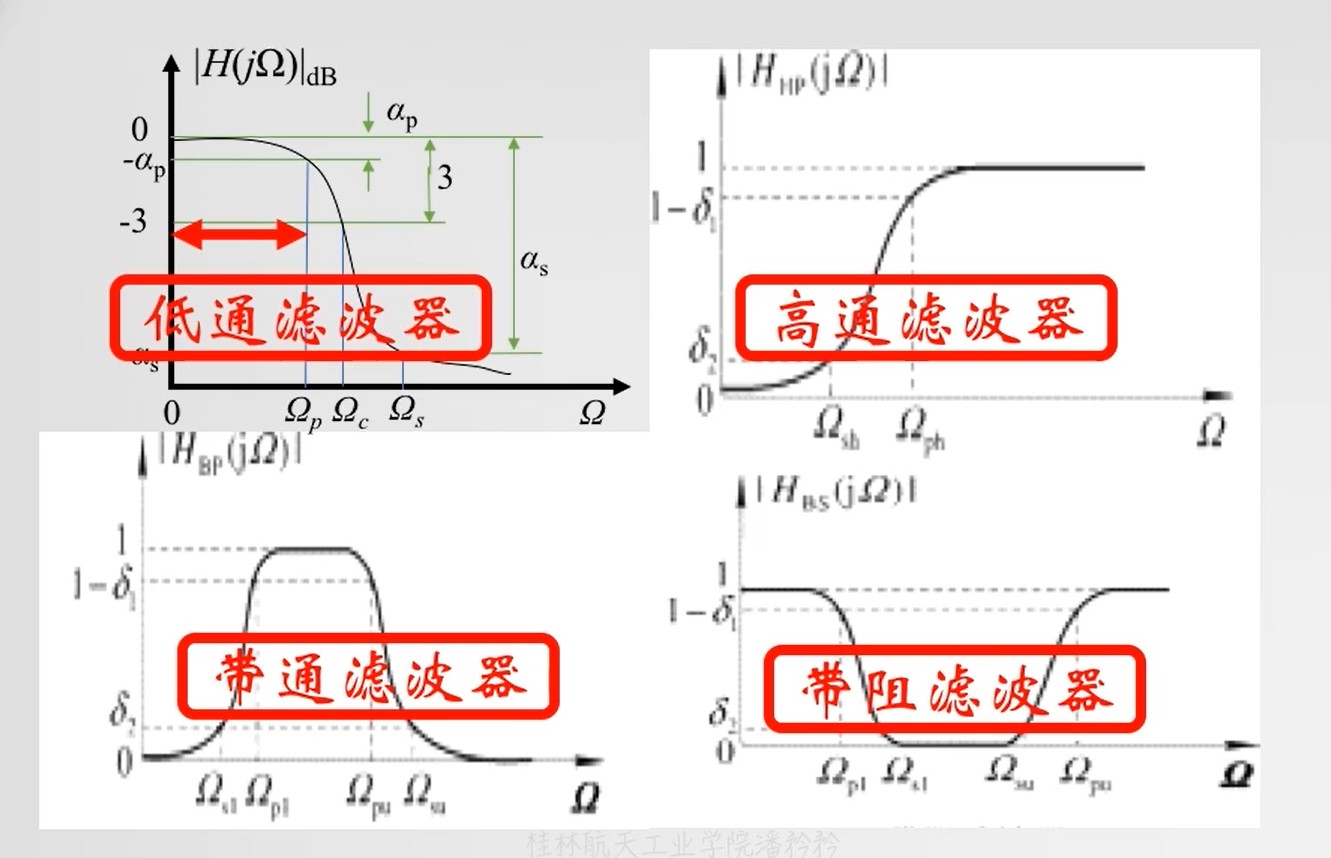
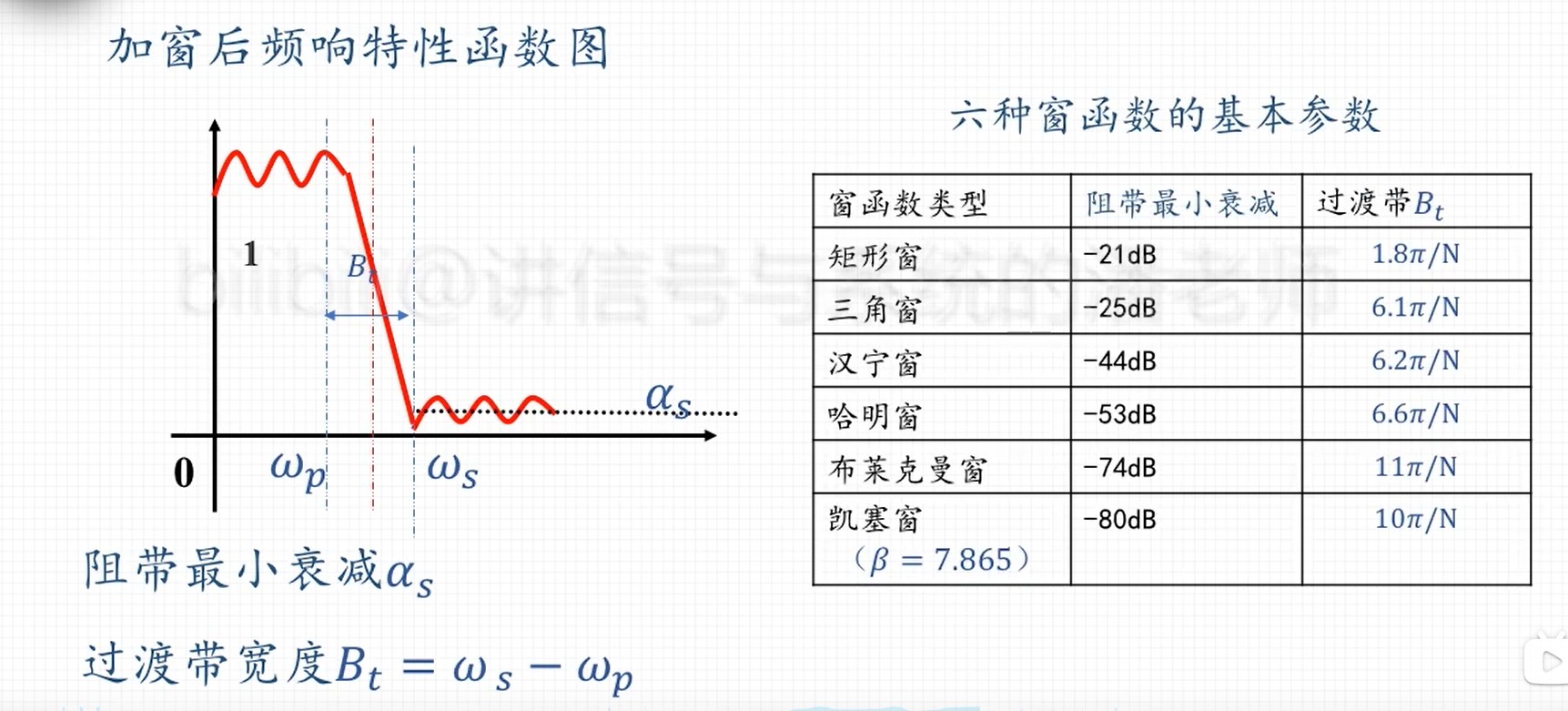
- 巴特沃斯滤波器
单调下降
- 切比雪夫滤波器
在通带或者阻带具有等波纹的特性,可提供选择性
- 椭圆滤波器
选择性好,但是通带内均匀呈现,等波纹幅频特性
- 贝塞尔滤波器
在通带内具有线性相位特性
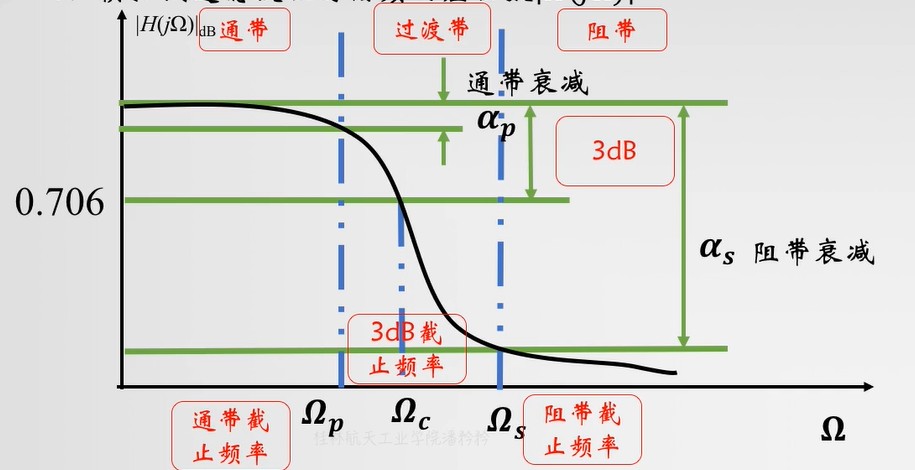
-
计算N
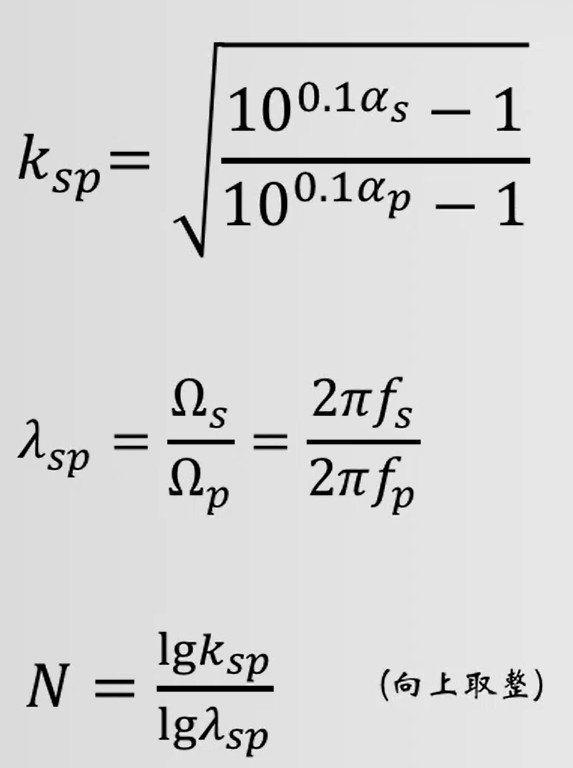
-
查表
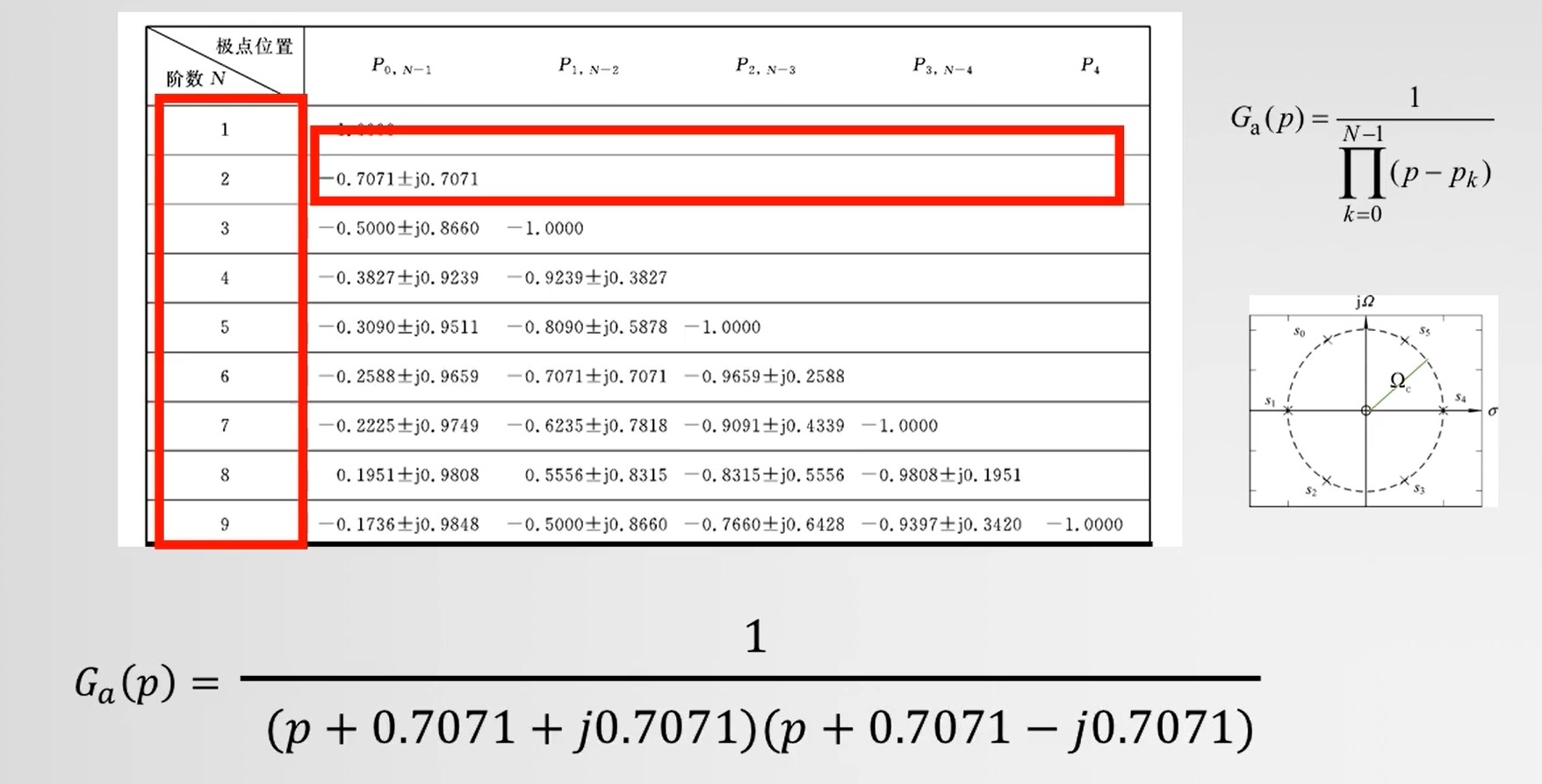
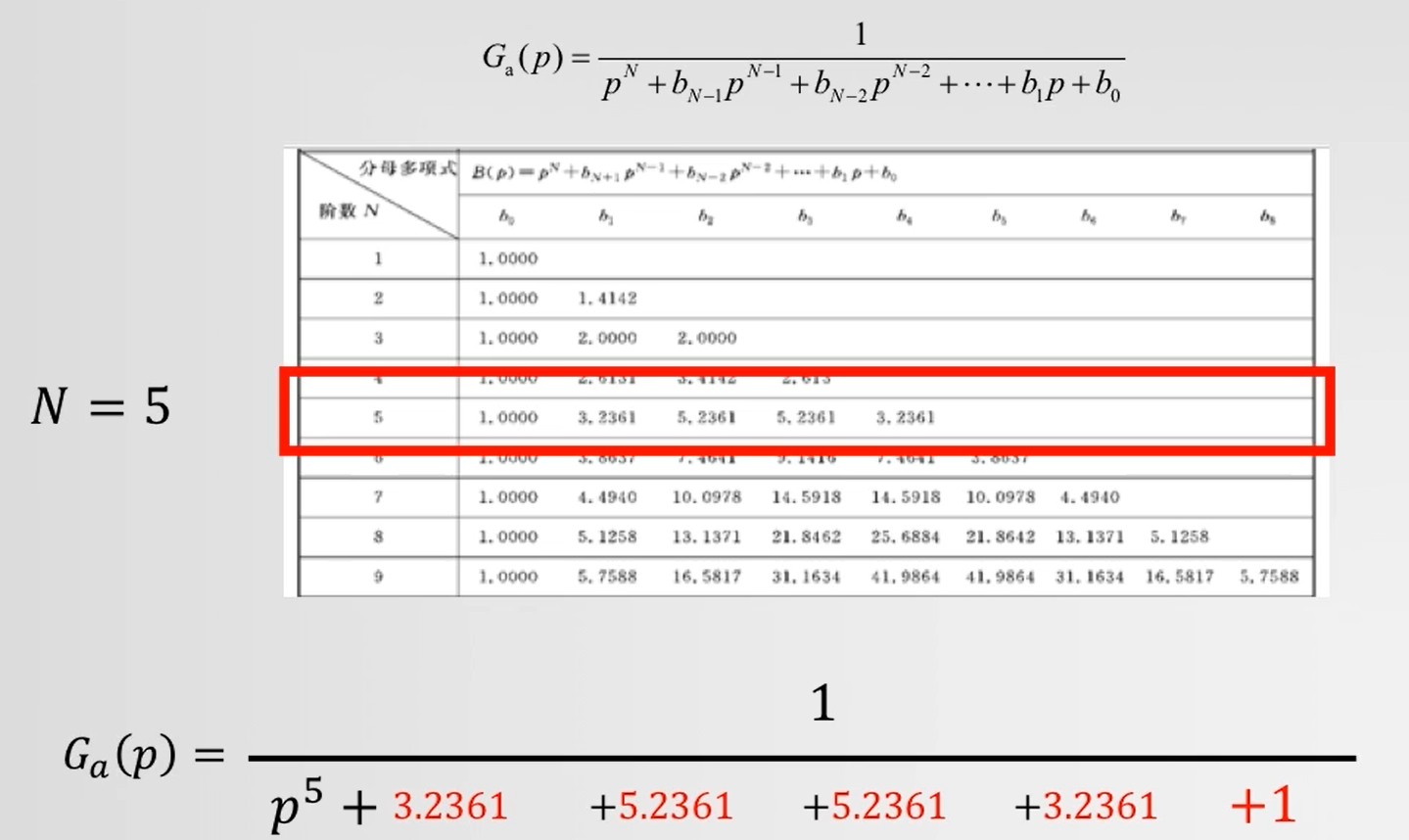
-
计算 Ωc
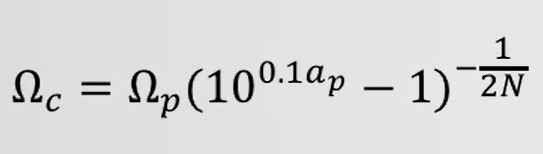
-
令 P=Ωcs 计算得到 Ha(s)=Ga(P)
根据奈奎斯特采样定理:fs≥2f, ω≤π ;数字信号频率:π 就对应着模拟信号的最高角频率。
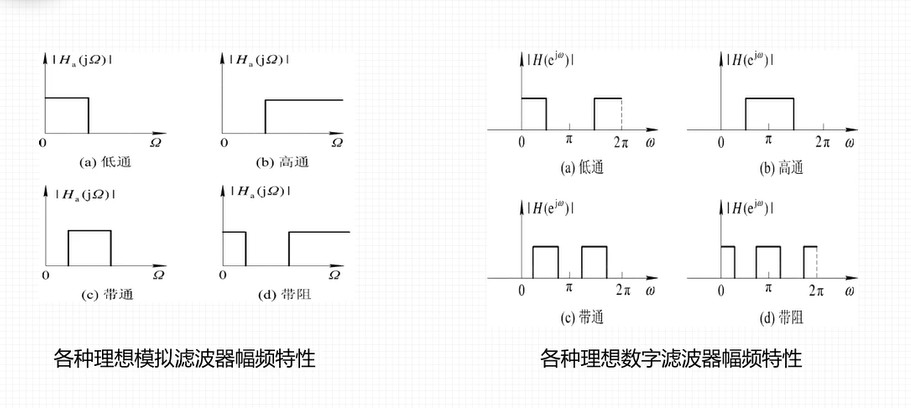
-
IIR滤波器 : 无限长脉冲响应数字滤波器
y(n)−k=0∑N−1aky(n−k)=k=0∑N−1bkx(n−k)(5.1)
H(z)=1+k=0∑Nbkz−kj=0∑Majz−j(5.2)
阶数由分母决定:N
-
FIR滤波器 : 有限长脉冲响应数字滤波器
y(n)=k=0∑N−1bkx(n−k)(5.3)
H(z)=k=0∑N−1h(k)z−k(5.4)
阶数为:N-1
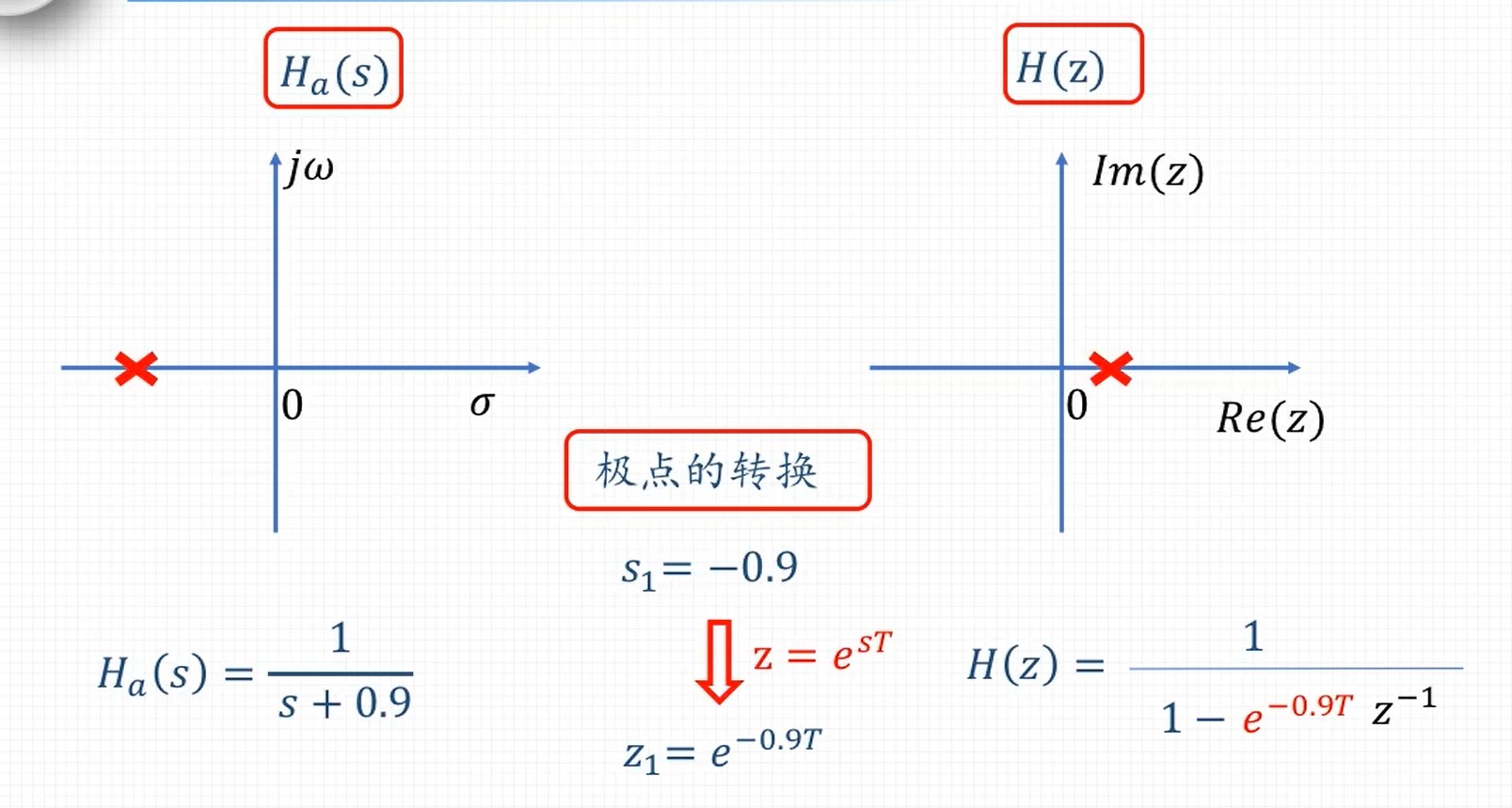
- 使用模拟滤波器的设计方法,设计出系统函数:Ha(s)
- 将 Ha(s) 转换为 H(z)
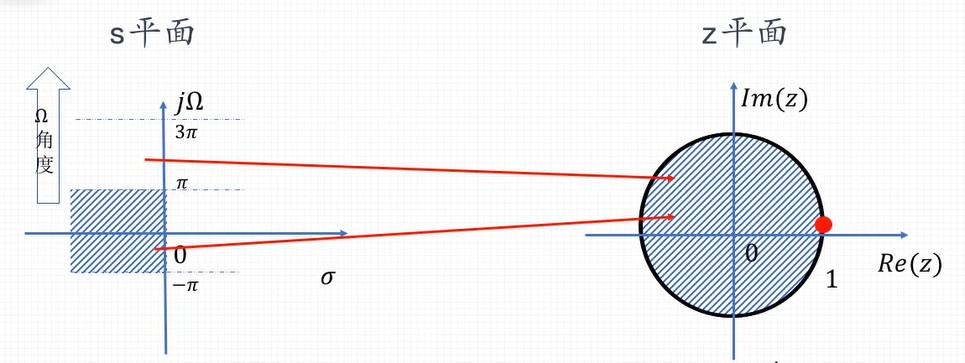
高通转为低通进行设计:
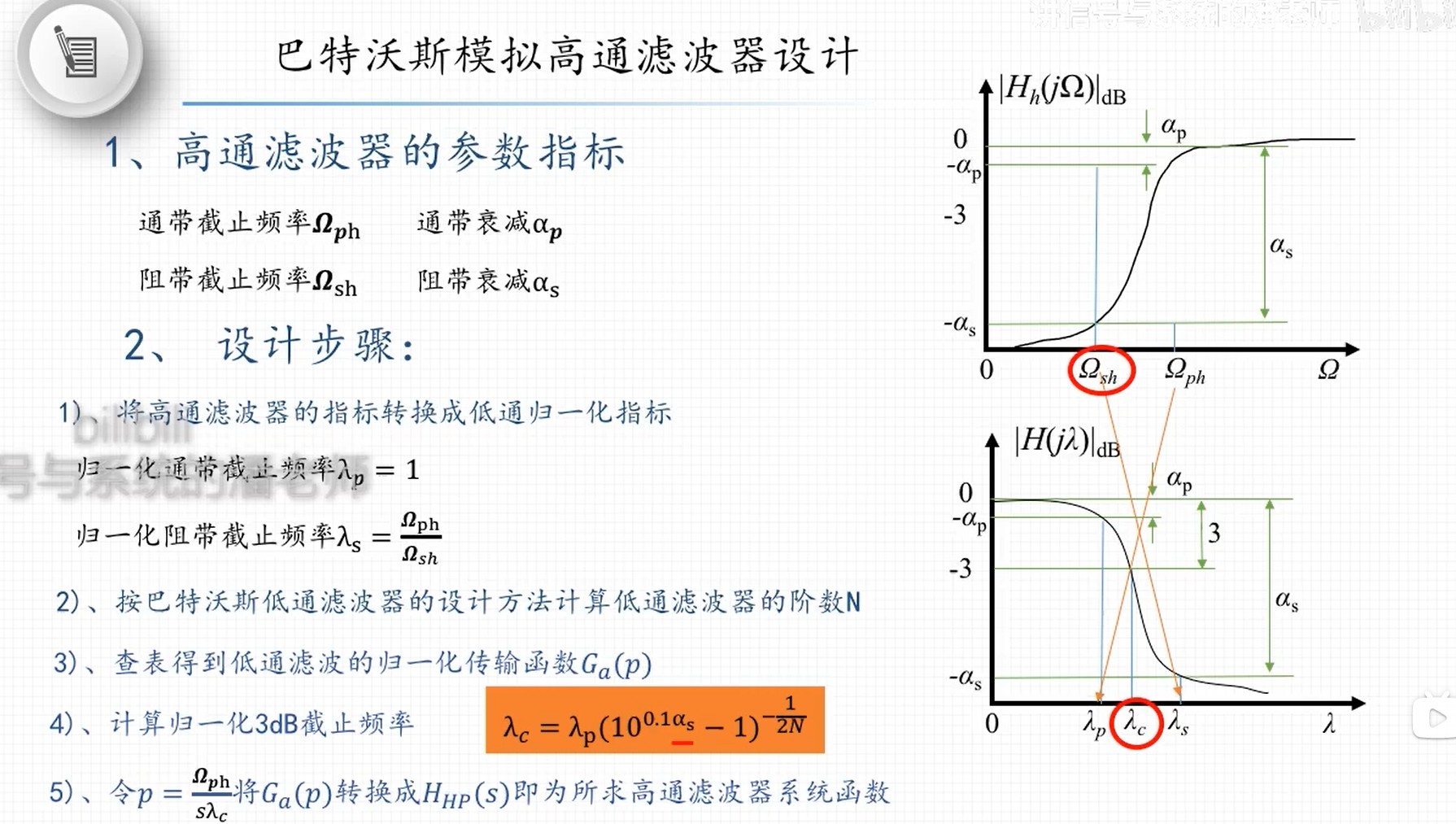
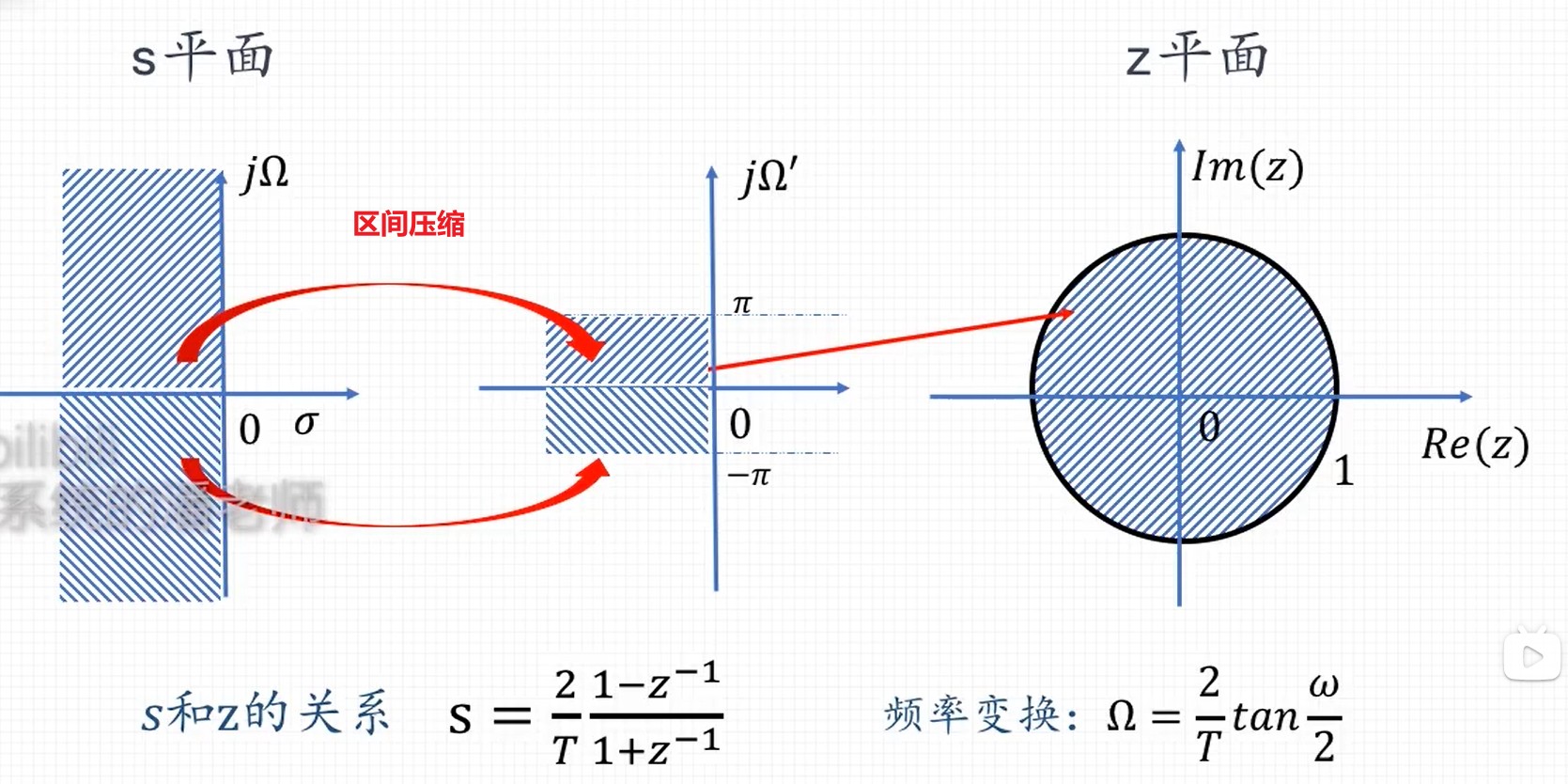
双线性法求解数字滤波器
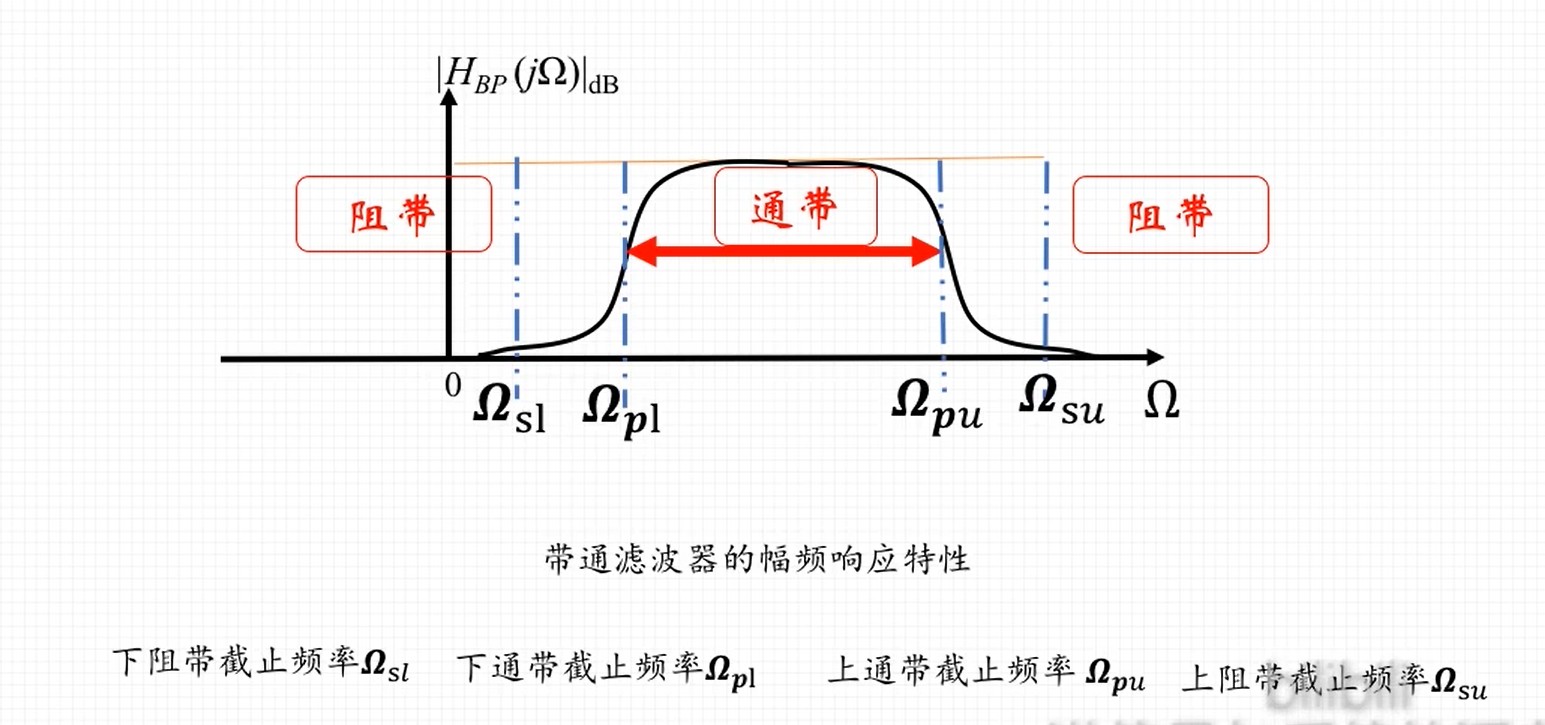
y(n)=k=0∑N−1bkx(n−k)(9.1)
H(z)=k=0∑N−1bkz−k(9.2)
零点:k=0∑N−1bkz−k=0,有N-1个
极点:1=1+k=0∑N−1akz−k,即极点z−k=0
通过时域公式可知,FIR滤波器是因果的;极点在单位圆内。故FIR恒稳定。